CS231N作业assignment1之SVM部分

Posted on | Edited on | In , ,

Assignment from: http: // cs231n.github.io / assignments2018 / assignment1/

目标：

  • a fully - vectorized loss function for the SVM
  • fully - vectorized expression for its analytic gradient
  • use a validation set to tune the learning rate and regularization strength
  • optimize the loss function with SGD
  • visualize the final learned weights

Set up部分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Run some setup code for this notebook.
from __future__ import print_function

import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt


# This is a bit of magic to make matplotlib figures appear inline in the
# notebook rather than in a new window.
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0)  # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

# Some more magic so that the notebook will reload external python modules;
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2

读取CIFAR-10的数据，预处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Load the raw CIFAR-10 data.
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'

# Cleaning up variables to prevent loading data multiple times (which may cause memory issue)
try:
  del X_train, y_train
  del X_test, y_test
  print('Clear previously loaded data.')
except:
  pass

X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)

# As a sanity check, we print out the size of the training and test data.
print('Training data shape: ', X_train.shape)
print('Training labels shape: ', y_train.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)

结果：

1
2
3
4
Training data shape: (50000, 32, 32, 3)
Training labels shape: (50000,)
Test data shape: (10000, 32, 32, 3)
Test labels shape: (10000,)

可视化dataset

  • 从类型中
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    # Visualize some examples from the dataset.
    # We show a few examples of training images from each class.
    classes = ['plane', 'car', 'bird', 'cat', 'deer',
               'dog', 'frog', 'horse', 'ship', 'truck']
    num_classes = len(classes)
    samples_per_class = 7
    for y, cls in enumerate(classes):
      idxs = np.flatnonzero(y_train == y)
      idxs = np.random.choice(idxs, samples_per_class, replace=False)
      for i, idx in enumerate(idxs):
        plt_idx = i * num_classes + y + 1
        plt.subplot(samples_per_class, num_classes, plt_idx)
        plt.imshow(X_train[idx].astype('uint8'))
        plt.axis('off')
        if i == 0:
          plt.title(cls)
    plt.show()
1
np.flatnonzero(y_train == y)

返回内容非0的index。这句是返回plane类别里面的（y_train == y）所有非0的内容。然后从这些里面随机选择7个内容，画出来。

结果如下：
可视化

进一步分为几部分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# Split the data into train, val, and test sets. In addition we will
# create a small development set as a subset of the training data;
# we can use this for development so our code runs faster.
num_training = 49000
num_validation = 1000
num_test = 1000
# 用这部分来优化代码
num_dev = 500

# Our validation set will be num_validation points from the original
# training set.
mask = range(num_training, num_training + num_validation)
X_val = X_train[mask]
y_val = y_train[mask]

# Our training set will be the first num_train points from the original
# training set.
mask = range(num_training)
X_train = X_train[mask]
y_train = y_train[mask]

# We will also make a development set, which is a small subset of
# the training set.
mask = np.random.choice(num_training, num_dev, replace=False)
X_dev = X_train[mask]
y_dev = y_train[mask]

# We use the first num_test points of the original test set as our
# test set.
mask = range(num_test)
X_test = X_test[mask]
y_test = y_test[mask]

print('Train data shape: ', X_train.shape)
print('Train labels shape: ', y_train.shape)
print('Validation data shape: ', X_val.shape)
print('Validation labels shape: ', y_val.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
1
2
mask = range(num_test)
X_test = X_test[mask]

感觉这是一种从一个整体中选取其中一部分的代码

将image拉成row

1
2
3
4
5
6
7
8
9
10
11
# Preprocessing: reshape the image data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_val = np.reshape(X_val, (X_val.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
X_dev = np.reshape(X_dev, (X_dev.shape[0], -1))

# As a sanity check, print out the shapes of the data
print('Training data shape: ', X_train.shape)
print('Validation data shape: ', X_val.shape)
print('Test data shape: ', X_test.shape)
print('dev data shape: ', X_dev.shape)
  • 当想把无论任何大小的东西拉成一整行的时候，用a.reshape(x, -1)。 X_train.shape[0]行，列数未知，但是拉平了
  • 如果想拉成一整列的时候，用a.reshape(-1, x)。 列数为x，每列有多少东西未知

预处理部分：减去mean image

  • 第一步，求出训练集的mean并且可视化

    1
    2
    3
    4
    5
    6
    7
    8
    # Preprocessing: subtract the mean image
    # first: compute the image mean based on the training data
    mean_image = np.mean(X_train, axis=0)
    print(mean_image[:10])  # print a few of the elements
    plt.figure(figsize=(4, 4))
    plt.imshow(mean_image.reshape((32, 32, 3)).astype(
        'uint8'))  # visualize the mean image
    plt.show()

  • 第二步，从train和test里面减去平均数据

    1
    2
    3
    4
    5
    # second: subtract the mean image from train and test data
    X_train -= mean_image
    X_val -= mean_image
    X_test -= mean_image
    X_dev -= mean_image

  • 第三步，把预处理好的所有图片的末尾（拉成行之后的最后）加了一个1（bias的dim）

    1
    2
    3
    4
    5
    6
    7
    8
    # third: append the bias dimension of ones (i.e. bias trick) so that our SVM
    # only has to worry about optimizing a single weight matrix W.
    X_train = np.hstack([X_train, np.ones((X_train.shape[0], 1))])
    X_val = np.hstack([X_val, np.ones((X_val.shape[0], 1))])
    X_test = np.hstack([X_test, np.ones((X_test.shape[0], 1))])
    X_dev = np.hstack([X_dev, np.ones((X_dev.shape[0], 1))])

    print(X_train.shape, X_val.shape, X_test.shape, X_dev.shape)

np.hstack()，沿着水平方向把数组叠起来。
于此相同，np.vstack()，是沿着垂直方向把数组叠起来。

SVM classifier

1
cs231n / classifiers / linear_svm.py.

svm_loss_naive

  • 有三个输入
    • X：一个有N个元素的minibatch，每个元素的内容是D(N, D)
    • W: weights，(D, C), 图片的内容是D，一共C个class，所以用的时候跟普遍想法的W是tranpose的
    • y: 标签，大小(N,) 一共N张照片，每张照片有一个标签
  • 最终结果
    • 一个float的结果：loss
    • W的gradient dW
  • 注意，Wx求出来的就是不同分类的积分

dW的计算(https://blog.csdn.net/zt_1995/article/details/62227201)

dW

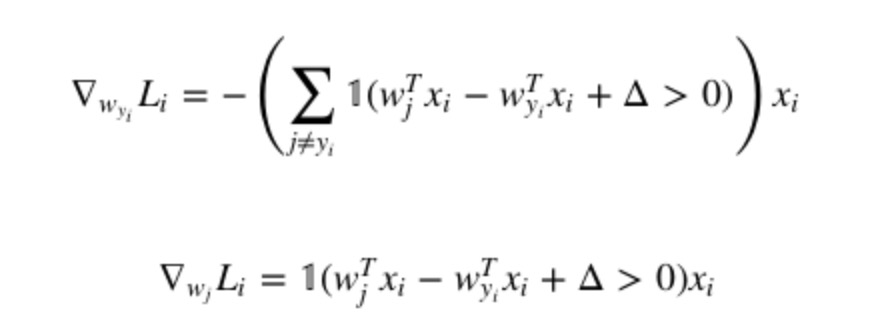
  • 形状很奇怪的1(x)指的是，当x为真的时候结果是1，当x为假的时候结果取0
  • 第一个式子表示第i个被正确分类的梯度
    • 有多少个Wj让这个边界值不被满足，就对损失起了多少贡献
    • 乘以xi是因为xi包含了样本的全部特征，所以前面乘以一个系数1就可以了
    • 符号是因为SGD采用负梯度运算
  • 第二个式子表示不正确分类的梯度，只有在yi == j的时候才有贡献，所以没有求和。但是注意，在每张图里面，这个都会在j == yi的时候发生一次，所以每张图的j部分需要加上这个值
  • 最终的结果需要，除以N
  • 别忘了正则化！而且用2\lanmdaW来正则化的效果更好一些
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51


def svm_loss_naive(W, X, y, reg):
  """
  Structured SVM loss function, naive implementation (with loops).

  Inputs have dimension D, there are C classes, and we operate on minibatches
  of N examples.

  Inputs:
  - W: A numpy array of shape (D, C) containing weights.
  - X: A numpy array of shape (N, D) containing a minibatch of data.
  - y: A numpy array of shape (N,) containing training labels; y[i] = c means
    that X[i] has label c, where 0 <= c < C.
  - reg: (float) regularization strength

  Returns a tuple of:
  - loss as single float
  - gradient with respect to weights W; an array of same shape as W
  """
  dW = np.zeros(W.shape)  # initialize the gradient as zero

  # compute the loss and the gradient
  num_classes = W.shape[1]
  # 有多少需要训练的个数
  num_train = X.shape[0]
  loss = 0.0
  for i in range(num_train):
    scores = X[i].dot(W)
    correct_class_score = scores[y[i]]
    for j in range(num_classes):
      # 如果这个类型是正确的，那就不用管了
      if j == y[i]:
        continue
      margin = scores[j] - correct_class_score + 1  # note delta = 1
      if margin > 0:
        loss += margin
        dW[:, y[i]] += -X[i]
        dW[:, j] += X[i]

  # Right now the loss is a sum over all training examples, but we want it
  # to be an average instead so we divide by num_train.
  loss /= num_train
  dW /= num_train

  # Add regularization to the loss.
  # reg是lanbda
  loss += reg * np.sum(W * W)
  dW += 2 * reg * W

  return loss, dW

svm_loss_vectorized

通过向量化来提高计算速度

计算loss部分

  • W是一个(D, C)的向量，X是(N, D)的，所以两者相乘可以得到一个(N, C)的矩阵，N为图片数量，C是每张图片对于不同分类的score
  • 在score中取每一行的y中label部分就是这张图正确类型的评分
  • 把整体的score矩阵的所有项减去正确评分的矩阵（应该可以广播但是我刚开始用repeat和reshape复制了一下），减去的结果就是svm中需要和0比的值（margin）
  • 为了求loss，把小于0的项目和正确的项除去（都设置成0）
  • 然后行求和，列求和，除以整体的个数，regularzation

计算dW部分

  • X.T点乘margin得到的就是最终的loss，所以需要把每个margin里面符合条件的数对了
  • 所有比0大的时候都算1（根据导数的计算结果）
  • 当应该判断正确的类型比0大的时候，这个东西会在每次计算导数的时候都算上一次，所以是行的合
  • 最后乘完之后除以总的个数，再regularzation
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47


    def svm_loss_vectorized(W, X, y, reg):
      """
      Structured SVM loss function, vectorized implementation.

      Inputs and outputs are the same as svm_loss_naive.
      """
      loss = 0.0
      dW = np.zeros(W.shape)  # initialize the gradient as zero

      #############################################################################
      # TODO:                                                                     #
      # Implement a vectorized version of the structured SVM loss, storing the    #
      # result in loss.                                                           #
      #############################################################################
      num_train = X.shape[0]
      num_classes = W.shape[1]
      scores = X.dot(W)
      # 这里是取第N行（图片行）的第C个（class列），得到的是（500，）的正确类的score的矩阵
      correct_class_score = scores[np.arange(num_train), y]
      # correct_class_score = np.repeat(correct_class_score, num_classes)
      # correct_class_score = correct_class_score.reshape(num_train, num_classes)

      # DxC
      margin = scores - correct_class_score + 1.0
      margin[np.arange(num_train), y] = 0.0
      margin[margin <= 0] = 0.0

      loss += np.sum(np.sum(margin, axis=1)) / num_train

      # loss /= num_train
      loss += 0.5 * reg * np.sum(W * W)


      margin[margin > 0] = 1.0
      calculate_times = np.sum(margin, axis=1)
      margin[np.arange(num_train), y] = - calculate_times

      dW = np.dot(X.T, margin) / num_train
      dW += 2 * reg * W

      #############################################################################
      #                             END OF YOUR CODE                              #
      #############################################################################

      return loss, dW

现在得到了dW和loss，使用SGD来减少loss

训练

  • 将整体分成不同的minibatch，使用np.random.choice，注意后面的replce可以选True，这样会重复选择元素但是结果速度好像是更快了
  • 将minibatch的结果计算loss和gradient，然后grad * learning rate来update数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
def train(self, X, y, learning_rate=1e-3, reg=1e-5, num_iters=100,
            batch_size=200, verbose=False):
    """
    Train this linear classifier using stochastic gradient descent.

    Inputs:
    - X: A numpy array of shape (N, D) containing training data; there are N
      training samples each of dimension D.
    - y: A numpy array of shape (N,) containing training labels; y[i] = c
      means that X[i] has label 0 <= c < C for C classes.
    - learning_rate: (float) learning rate for optimization.
    - reg: (float) regularization strength.
    - num_iters: (integer) number of steps to take when optimizing
    - batch_size: (integer) number of training examples to use at each step.
    - verbose: (boolean) If true, print progress during optimization.

    Outputs:
    A list containing the value of the loss function at each training iteration.
    """
    num_train, dim = X.shape
    # assume y takes values 0...K-1 where K is number of classes
    num_classes = np.max(y) + 1
    if self.W is None:
      # lazily initialize W
      self.W = 0.001 * np.random.randn(dim, num_classes)

    # Run stochastic gradient descent to optimize W
    loss_history = []
    for it in range(num_iters):
      X_batch = None
      y_batch = None

      #########################################################################
      # TODO:                                                                 #
      # Sample batch_size elements from the training data and their           #
      # corresponding labels to use in this round of gradient descent.        #
      # Store the data in X_batch and their corresponding labels in           #
      # y_batch; after sampling X_batch should have shape (dim, batch_size)   #
      # and y_batch should have shape (batch_size,)                           #
      #                                                                       #
      # Hint: Use np.random.choice to generate indices. Sampling with         #
      # replacement is faster than sampling without replacement.              #
      #########################################################################
      indices = np.random.choice(num_train, batch_size, replace=True)
      X_batch = X[indices]
      y_batch = y[indices]

      #########################################################################
      #                       END OF YOUR CODE                                #
      #########################################################################

      # evaluate loss and gradient
      loss, grad = self.loss(X_batch, y_batch, reg)
      loss_history.append(loss)

      # perform parameter update
      #########################################################################
      # TODO:                                                                 #
      # Update the weights using the gradient and the learning rate.          #
      #########################################################################
      self.W += - learning_rate * grad
      #########################################################################
      #                       END OF YOUR CODE                                #
      #########################################################################

      if verbose and it % 100 == 0:
        print('iteration %d / %d: loss %f' % (it, num_iters, loss))

    return loss_history

预测结果

  • 已经有了前面的到的训练过的W（self.W）
  • Wx算出来的就是分数
  • 从每一行里面选择最大的分数就是预测的结果
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    def predict(self, X):
        """
        Use the trained weights of this linear classifier to predict labels for
        data points.

        Inputs:
        - X: A numpy array of shape (N, D) containing training data; there are N
          training samples each of dimension D.

        Returns:
        - y_pred: Predicted labels for the data in X. y_pred is a 1-dimensional
          array of length N, and each element is an integer giving the predicted
          class.
        """
        y_pred = np.zeros(X.shape[0])
        ###########################################################################
        # TODO:                                                                   #
        # Implement this method. Store the predicted labels in y_pred.            #
        ###########################################################################
        scores = X.dot(self.W)
        y_pred = np.argmax(scores, axis=1)
        # print(labels.shape)
        # print(labels)
        ###########################################################################
        #                           END OF YOUR CODE                              #
        ###########################################################################
        return y_pred

交叉验证

  • 在作业里，需要选择两个hyper的值，分别是学习率和regularzation的参数，没有采用交叉验证，但是采用了随机搜索，会比grid search更准确一些
  • 采用不同的参数组合分别训练这个模型，然后得到各自在validation上面的准确率，这个得到准确率最大的组合的参数
  • 注意，在验证的过程中应该选择iter的次数少一点，不然训练的时间会非常长
  • 在这个代码里用了rand来得到0到1之间的随机数，这个数乘以hyper的范围的差，然后再加上下限，就是随机得到的最终结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
rand_turple = np.random.rand(50,2)
rand_turple[:,0] = rand_turple[:,0]*(learning_rates[1]-learning_rates[0]) + learning_rates[0]
rand_turple[:,1] = rand_turple[:,1]*(regularization_strengths[1]-regularization_strengths[0])+regularization_strengths[0]
for lr,rs in rand_turple:
    svm = LinearSVM()
    svm.train(X_train, y_train, learning_rate=lr, reg=rs,num_iters=1500, verbose=True)
    y_train_pred = svm.predict(X_train)
    train_acc = np.mean(y_train == y_train_pred)
    y_val_pred = svm.predict(X_train)
    val_acc = np.mean(y_train == y_val_pred)
    results[(lr,rs)] = (train_acc,val_acc)
    if (val_acc > best_val):
        best_val = val_acc
        best_svm = svm

结果可视化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Visualize the learned weights for each class.
# Depending on your choice of learning rate and regularization strength, these may
# or may not be nice to look at.
w = best_svm.W[:-1,:] # strip out the bias
w = w.reshape(32, 32, 3, 10)
w_min, w_max = np.min(w), np.max(w)
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
for i in range(10):
    plt.subplot(2, 5, i + 1)
      
    # Rescale the weights to be between 0 and 255
    wimg = 255.0 * (w[:, :, :, i].squeeze() - w_min) / (w_max - w_min)
    plt.imshow(wimg.astype('uint8'))
    plt.axis('off')
    plt.title(classes[i])

可视化结果