CS231Nassignment1之two_layer_net

目标

• Implement a neural network with fc layers for classifiction
• Test it on CIFAR-10 dataset

初始化

auto-reloading external modules

定义relative error

def rel_error(x, y):
    """ returns relative error """
    return np.max(np.abs(x - y) / (np.maximum(1e-8, np.abs(x) + np.abs(y))))

• 这里插入一下np.max和np.maximum的区别
  • max是求序列的最值，可以输入一个参数，axis表示的是求最值的方向
  • maximum至少输入两个参数，会把两个参数逐位比较，然后输出比较大的那个结果
• 但是好像在这里的使用上面，说明x和y不是一个单独的值，应该是两个数组

>> np.max([-4, -3, 0, 0, 9])
9

>> np.maximum([-3, -2, 0, 1, 2], 0)
array([0, 0, 0, 1, 2])

不是很理解这里为什么要除以x+y

设置参数

cs231n/classifiers/neural_net.py
self.params储存了需要的参数，参数都被存储在dict里面，一个名字对应一个内容

两层神经网络的参数如下：

• W1，第一层的weights，（D，H），其中H是第二层的neruon的个数。因为只有一层的时候，D个输入对应C个输出，现在有两层的fc，对应的输出就是第二层的units个数
• b1，第一层的bias，（H，）
• W2，第二层的weights，（H，C）
• b2，第二层的bias
  bias都需要初始化为相应大小的0，weights初始化成0-1之间的比较小的数字

Forward pasa

计算scores

• 这部分非常简单，两次Wx+b，并且在第一次之后记得激活就可以了
• 激活函数用的relu，内容就是score小于0的部分让他直接等于0

计算loss

• 这里用的是softmax计算loss，和softmax的作业内容一样，将所有的scores exp，求占的百分比，求出来的部分-log，然后把所有的求和
• 这里用到了boardcasting的问题，注意（100，1）这样的才可以boardcasting，（100，）的是一维数组，需要把它reshape成前面的样子才可以
• 这里最后的结果还总是差一点，最后发现是因为regularzation的时候多乘了0.5，看题呜呜呜

Backward pass

• 由于b是线性模型的bias，偏导数是1，直接对class的内容求和然后除以N就是最终结果
• 对W求导的时候需要用到链式法则，然后直接代码实现一下就行了
• 这里遇到的主要问题是loss的值会影响他估计的值，因为loss的regularzation改了，所以答案一直对不上。

Training predict

• 训练和之前写的差不多，训练网络，主要包括写training部分的随机mini-batch和更新weights，记得lr更新的时候要带负号
• 预测也差不多，算出来scores，找到最大的score就是分类的结果。注意找最大的时候要用argmax，找到的是最大的东西的indice，不然得到的是得分

  net = init_toy_model()
  stats = net.train(X, y, X, y,
              learning_rate=1e-1, reg=5e-6,
              num_iters=100, verbose=False)
  
  print('Final training loss: ', stats['loss_history'][-1])
  
  # plot the loss history
  plt.plot(stats['loss_history'])
  plt.xlabel('iteration')
  plt.ylabel('training loss')
  plt.title('Training Loss history')
  plt.show()

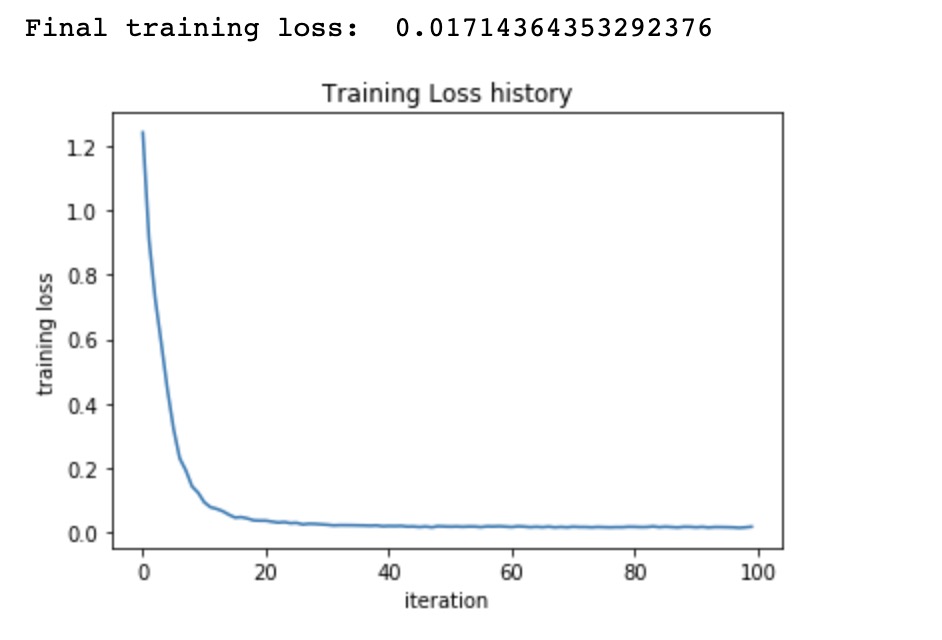
使用写好的来训练CIFAR-10

input_size = 32 * 32 * 3
hidden_size = 50
num_classes = 10
net = TwoLayerNet(input_size, hidden_size, num_classes)

# Train the network
stats = net.train(X_train, y_train, X_val, y_val,
            num_iters=1000, batch_size=200,
            learning_rate=1e-4, learning_rate_decay=0.95,
            reg=0.25, verbose=True)

# Predict on the validation set
val_acc = (net.predict(X_val) == y_val).mean()
print('Validation accuracy: ', val_acc)

这时候得到的准确度应该在28%左右，可以优化

进一步优化

• 一种可视化的方法是可视化loss function和准确率的关系，分别在训练和val集上面
• 另种是可视化第一层的weights

两种方法的结果如下：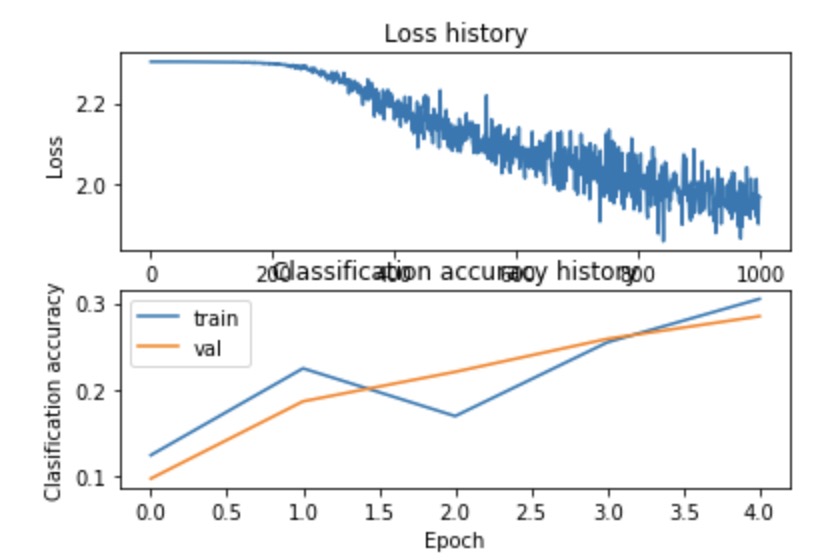

debug模型

• 问题
  • loss大体上都是linearly的下降的，说明lr可能太低了
  • 在training和val的准确率上没有gap，说明model的容量太小的，需要增大size
  • 如果容量过大还会导致overfiiting，这时候gap就会很大
• tuning hypers
  • 题目里面的建议是tuning几个hyper，还是和之前一样，直接random，search
  • 这里选了三个参数，分别是units的数量，learning rate和reg的强度，随便设置了一下界限
  • 最终计算出来的val准确率是：49.5% 秀秀秀！！
  • 可视化weigh之后的结果是

• 震惊，居然最后的测试正确率也达到了49.4！！！

best_net = None # store the best model into this 

#################################################################################
# TODO: Tune hyperparameters using the validation set. Store your best trained  #
# model in best_net.                                                            #
#                                                                               #
# To help debug your network, it may help to use visualizations similar to the  #
# ones we used above; these visualizations will have significant qualitative    #
# differences from the ones we saw above for the poorly tuned network.          #
#                                                                               #
# Tweaking hyperparameters by hand can be fun, but you might find it useful to  #
# write code to sweep through possible combinations of hyperparameters          #
# automatically like we did on the previous exercises.                          #
#################################################################################
best_acc = -1

learning_rates = [1e-3, 1e-2]
regularization_strengths = [1e-2, 6e-1]
hidden_size = [50, 150]


random_search = np.random.rand(30, 3)
random_search[:, 0] = random_search[:, 0] * \
    (learning_rates[1] - learning_rates[0]) + learning_rates[0]
random_search[:, 1] = random_search[:, 1] * \
    (regularization_strengths[1] - regularization_strengths[0]
     ) + regularization_strengths[0]
random_search[:, 2] = random_search[:, 2] * \
    (hidden_size[1] - hidden_size[0]) + hidden_size[0]

for lr, rs, hidd in random_search:
  input_size = 32 * 32 * 3
  hidden = int(hidd)
  num_class = 10

  net = TwoLayerNet(input_size, hidden, num_class)

  status = net.train(X_train, y_train, X_val, y_val, num_iters=1000, batch_size=200,
                     learning_rate=lr, learning_rate_decay=0.95, reg=rs, verbose=True)

  val_acc = (net.predict(X_val) == y_val).mean()

  if val_acc > best_acc:
    best_acc = val_acc
    best_net = net

print("best net is with val acc", best_acc)

#################################################################################
#                               END OF YOUR CODE                                #
#################################################################################

代码部分

nerual_net.py部分的完整代码如下

from __future__ import print_function

import numpy as np
import matplotlib.pyplot as plt


class TwoLayerNet(object):
  """
  A two-layer fully-connected neural network. The net has an input dimension of
  N, a hidden layer dimension of H, and performs classification over C classes.
  We train the network with a softmax loss function and L2 regularization on the
  weight matrices. The network uses a ReLU nonlinearity after the first fully
  connected layer.

  In other words, the network has the following architecture:

  input - fully connected layer - ReLU - fully connected layer - softmax

  The outputs of the second fully-connected layer are the scores for each class.
  """

  def __init__(self, input_size, hidden_size, output_size, std=1e-4):
    """
    Initialize the model. Weights are initialized to small random values and
    biases are initialized to zero. Weights and biases are stored in the
    variable self.params, which is a dictionary with the following keys:

    W1: First layer weights; has shape (D, H)
    b1: First layer biases; has shape (H,)
    W2: Second layer weights; has shape (H, C)
    b2: Second layer biases; has shape (C,)

    Inputs:
    - input_size: The dimension D of the input data.
    - hidden_size: The number of neurons H in the hidden layer.
    - output_size: The number of classes C.
    """
    self.params = {}
    self.params['W1'] = std * np.random.randn(input_size, hidden_size)
    self.params['b1'] = np.zeros(hidden_size)
    self.params['W2'] = std * np.random.randn(hidden_size, output_size)
    self.params['b2'] = np.zeros(output_size)

  def loss(self, X, y=None, reg=0.0):
    """
    Compute the loss and gradients for a two layer fully connected neural
    network.

    Inputs:
    - X: Input data of shape (N, D). Each X[i] is a training sample.
    - y: Vector of training labels. y[i] is the label for X[i], and each y[i] is
      an integer in the range 0 <= y[i] < C. This parameter is optional; if it
      is not passed then we only return scores, and if it is passed then we
      instead return the loss and gradients.
    - reg: Regularization strength.

    Returns:
    If y is None, return a matrix scores of shape (N, C) where scores[i, c] is
    the score for class c on input X[i].

    If y is not None, instead return a tuple of:
    - loss: Loss (data loss and regularization loss) for this batch of training
      samples.
    - grads: Dictionary mapping parameter names to gradients of those parameters
      with respect to the loss function; has the same keys as self.params.
    """
    # Unpack variables from the params dictionary
    W1, b1 = self.params['W1'], self.params['b1']
    W2, b2 = self.params['W2'], self.params['b2']
    N, D = X.shape

    # Compute the forward pass
    scores = None
    #############################################################################
    # TODO: Perform the forward pass, computing the class scores for the input. #
    # Store the result in the scores variable, which should be an array of      #
    # shape (N, C).                                                             #
    #############################################################################

    # first layer, shape(N,H)
    X1 = X.dot(W1) + b1

    # 这里加了一个第一层之后的relu激活
    relu = np.maximum(0, X1)
    # final result, shape(N,C)
    scores = relu.dot(W2) + b2
    #############################################################################
    #                              END OF YOUR CODE                             #
    #############################################################################

    # If the targets are not given then jump out, we're done
    if y is None:
      return scores

    # Compute the loss
    loss = None
    #############################################################################
    # TODO: Finish the forward pass, and compute the loss. This should include  #
    # both the data loss and L2 regularization for W1 and W2. Store the result  #
    # in the variable loss, which should be a scalar. Use the Softmax           #
    # classifier loss.                                                          #
    #############################################################################

    num_train = N

    scores = scores - np.reshape(np.max(scores, axis=1), (num_train, -1))

    scores = np.exp(scores)
    scores_sum = np.sum(scores, axis=1).reshape(N, 1)
    # scores_sum = np.sum(scores, axis=1, keepdims=True)
    p = scores / scores_sum

    loss = np.sum(-np.log(p[np.arange(N), y]))
    loss /= num_train
    # 这里不要乘0.5的系数
    # loss += reg * np.sum(W1 * W1) + reg * np.sum(W2 * W2)

    loss += 0.5 * reg * np.sum(W1 * W1) + 0.5 * reg * np.sum(W2 * W2)

    # #############################################################################
    # #                              END OF YOUR CODE                             #
    # #############################################################################

    # # Backward pass: compute gradients
    grads = {}
    # #############################################################################
    # # TODO: Compute the backward pass, computing the derivatives of the weights #
    # # and biases. Store the results in the grads dictionary. For example,       #
    # # grads['W1'] should store the gradient on W1, and be a matrix of same size #
    # #############################################################################

    dscores = p
    dscores[range(N), y] -= 1.0
    # dscores /= N

    # shape dW2(CxN) x(NxH) -> (CxH)
    # dW2 = np.dot(relu.T, p)
    dW2 = np.dot(relu.T, dscores)
    # print(dW2)

    # 每个class会有一个b，对b求导是1
    # shape db2 (C,)
    db2 = np.sum(p, axis=0)

    # (NxC) x (HxC).T -> (N,H)
    dW_relu = np.dot(dscores, W2.T)
    dW_relu[relu <= 0] = 0

    # (NxD).T x (N,H) -> (D,H)
    dW1 = (X.T).dot(dW_relu)
    db1 = np.sum(dW_relu, axis=0)

    dW2 /= N
    dW1 /= N
    dW2 += reg * W2
    dW1 += reg * W1

    db1 /= N
    db2 /= N

    grads['W1'] = dW1
    grads['b1'] = db1
    grads['W2'] = dW2
    grads['b2'] = db2

    #############################################################################
    # END OF YOUR CODE #
    #############################################################################

    return loss, grads

  def train(self, X, y, X_val, y_val,
            learning_rate=1e-3, learning_rate_decay=0.95,
            reg=5e-6, num_iters=100,
            batch_size=200, verbose=False):
    """
    Train this neural network using stochastic gradient descent.

    Inputs:
    - X: A numpy array of shape (N, D) giving training data.
    - y: A numpy array f shape (N,) giving training labels; y[i] = c means that
      X[i] has label c, where 0 <= c < C.
    - X_val: A numpy array of shape (N_val, D) giving validation data.
    - y_val: A numpy array of shape (N_val,) giving validation labels.
    - learning_rate: Scalar giving learning rate for optimization.
    - learning_rate_decay: Scalar giving factor used to decay the learning rate
      after each epoch.
    - reg: Scalar giving regularization strength.
    - num_iters: Number of steps to take when optimizing.
    - batch_size: Number of training examples to use per step.
    - verbose: boolean; if true print progress during optimization.
    """
    num_train = X.shape[0]
    iterations_per_epoch = max(num_train / batch_size, 1)

    # Use SGD to optimize the parameters in self.model
    loss_history = []
    train_acc_history = []
    val_acc_history = []

    for it in range(num_iters):
      X_batch = None
      y_batch = None

      #########################################################################
      # TODO: Create a random minibatch of training data and labels, storing  #
      # them in X_batch and y_batch respectively.                             #
      #########################################################################
      rand_mini = np.random.choice(num_train, batch_size, replace=True)
      X_batch = X[rand_mini]
      y_batch = y[rand_mini]

      #########################################################################
      #                             END OF YOUR CODE                          #
      #########################################################################

      # Compute loss and gradients using the current minibatch
      loss, grads = self.loss(X_batch, y=y_batch, reg=reg)
      loss_history.append(loss)

      #########################################################################
      # TODO: Use the gradients in the grads dictionary to update the         #
      # parameters of the network (stored in the dictionary self.params)      #
      # using stochastic gradient descent. You'll need to use the gradients   #
      # stored in the grads dictionary defined above.                         #
      #########################################################################
      self.params['W1'] -= learning_rate * grads['W1']
      self.params['W2'] -= learning_rate * grads['W2']
      self.params['b1'] -= learning_rate * grads['b1']
      self.params['b2'] -= learning_rate * grads['b2']
      #########################################################################
      #                             END OF YOUR CODE                          #
      #########################################################################

      if verbose and it % 100 == 0:
        print('iteration %d / %d: loss %f' % (it, num_iters, loss))

      # Every epoch, check train and val accuracy and decay learning rate.
      if it % iterations_per_epoch == 0:
        # Check accuracy
        train_acc = (self.predict(X_batch) == y_batch).mean()
        val_acc = (self.predict(X_val) == y_val).mean()
        train_acc_history.append(train_acc)
        val_acc_history.append(val_acc)

        # Decay learning rate
        learning_rate *= learning_rate_decay

    return {
        'loss_history': loss_history,
        'train_acc_history': train_acc_history,
        'val_acc_history': val_acc_history,
    }

  def predict(self, X):
    """
    Use the trained weights of this two-layer network to predict labels for
    data points. For each data point we predict scores for each of the C
    classes, and assign each data point to the class with the highest score.

    Inputs:
    - X: A numpy array of shape (N, D) giving N D-dimensional data points to
      classify.

    Returns:
    - y_pred: A numpy array of shape (N,) giving predicted labels for each of
      the elements of X. For all i, y_pred[i] = c means that X[i] is predicted
      to have class c, where 0 <= c < C.
    """
    y_pred = None

    ###########################################################################
    # TODO: Implement this function; it should be VERY simple!                #
    ###########################################################################
    W1 = self.params['W1']
    W2 = self.params['W2']
    b1 = self.params['b1']
    b2 = self.params['b2']

    scores = X.dot(W1) + b1
    scores[scores < 0] = 0.0
    scores = scores.dot(W2) + b2

    y_pred = np.argmax(scores, axis=1)
    ###########################################################################
    #                              END OF YOUR CODE                           #
    ###########################################################################

    return y_pred