本文参考支持向量机通俗导论内容
SVM到底是啥
support vecttor machine,比如在二维平面上,要把一个东西分成两类,SVM就是平面上的一条直线,并且在这两类的正中间,离两边一样远。换句话说,学习策略是把间隔最大化,从而得到凸二次规划问题的解(虽然不是很理解,但是凸问题应该是比较好求解)
分类标准 logistic regression
- 线性分类器:x表示数据,y表示类别,分类器则需要在n维找到一个超平面hyper plane,超平面的方程就是W.T
- 也就是 W.T.dot(x) + b = 0
(令人震惊w居然是超平面的方程)
逻辑回归
- 逻辑回归就是从特征里面学到一个0/1的分类模型
- 模型的线性组合作为自变量,取值范围是负无穷到正无穷,所以使用logistic函数(竟然就是si
moid函数把他们投影到(0,1)上面,得到的值就是y = 1的概率 - 线性分类器如果把分类的两类改成 -1和1(只是为了方便选了这个数字),其实就是把wx加了b
- 这时候的点的位置可以用 f(x) = wx + b表示,如果f(x)等于0,那么这个点在超平面上,如果大于0就是在1的类型里,小于0在-1的类型里
- 这时候问题变成了寻找间隔最大的超平面
function margin,geometrical margin
函数距离
- 当平面上的点是 wx+b = 0 确定了以后, wx+b的绝对值就是点x到超平面的距离
- 同时 wx+b 的符号和 y(分类标签)的符号对比,如果一致的话是一个类别,不一致的话是另一个 -> y(wx+ b)的正负来表示分类的正确与否 (也就是两个东西同号得正分类正确)
- 引出函数间隔的定义(这里的y是乘上对应类别的y,所以能得到绝对值)
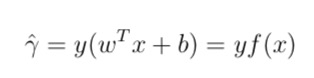
在训练集中,所有点到超平面的距离的最小点就是function margin
几何距离
- 但是如果单纯这么评定,当w和b成比例改变的时候,函数间隔也会改变,所以还需要几何间隔
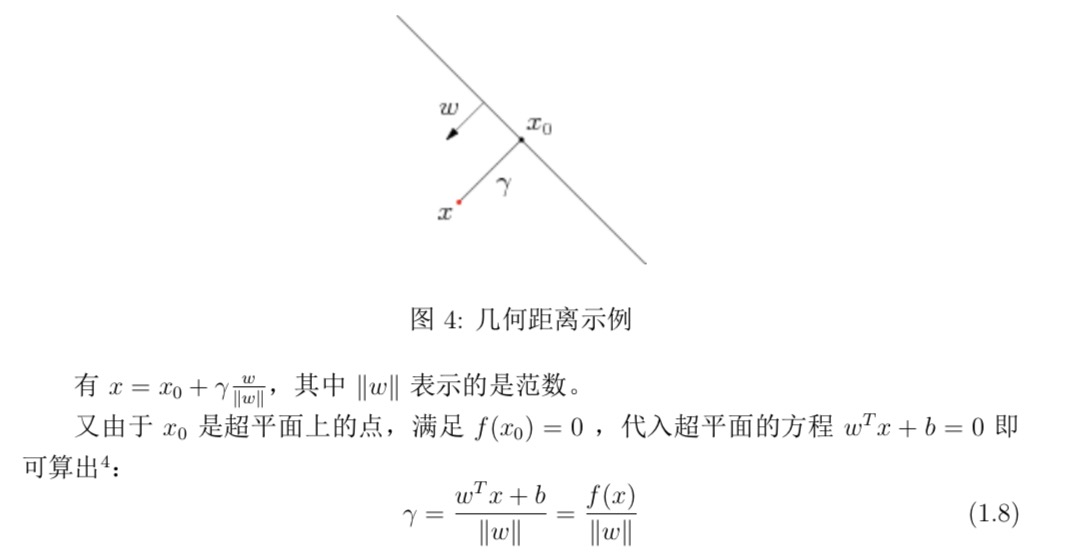
上面的式子乘以y(对应类别的标签)就可以得到绝对值了。
也就是说几何margin的主要部分就是把之前的内容除了一个w的范数,变成了标准化之后的长度
最大间隔分类器 max margin classifier
对于一组数据来说,超平面和数据点的距离越大,这个数据的分类确信度(confidence)就越高
- 最大的间距的目标函数即: max\gama, 其中gama是比所有其他间隔都短的函数间隔
- 如果让最小的函数间隔等于1(为了方便计算),然后求几何间隔,可以得知需要的目标函数变为最大化 1/||w||,其中w是超平面
深入SVM
线性可分和不可分
原始问题和对偶问题duality
- 之前的目标函数是
1/||w||,所以求这个的最大值,就是求1/2*||w||^2的最小值(这里求最大值就是求倒数的最小值,然后1/2和平方都是为了方便加的) - 目标函数变成二次的,约束条件是线性的,凸二次问题,可以用QP(一个写的差不多的包) -> 目标最优的时候loss
- 由于这个问题的结构,可以转换成对偶问题求解
- 给每一个约束条件加上一个拉格朗日乘子 alpha
- 把这个融合进入目标函数里面
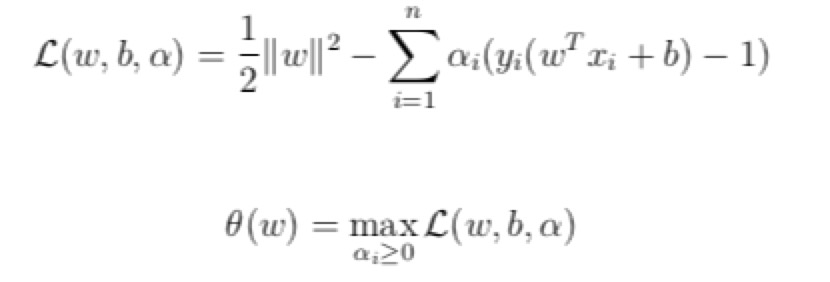
- 当所有的约束条件都满足的时候,目标函数的结果就是之前需要求的目标函数。
- 再对这个目标函数(新的)求最小值,得到的结果就是本来需要求的最小值
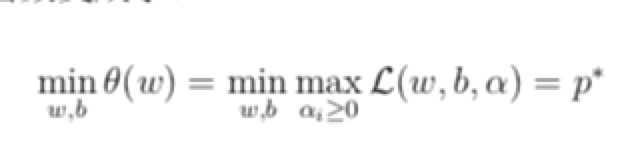
- 最后,因为上面的问题不是很好求解,把它的max和min交换了一下,先求所有的间隔的最小值,然后再求这里面alpha条件可以满足的最大值,这两个问题就是对偶问题
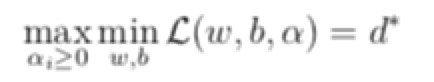
- d <= p ,在某些条件满足的情况下这两个值相等,这时候求出来对偶问题就可以求出来原始问题的解
- 转换对偶问题的原因:
- 对偶问题更容易求解
- 可以引入核函数,这样可以直接引入非线性问题
K.K.T条件
- 上一段说的,满足对偶问题的解等价的条件就是KKT条件
- KTT条件的意义:非线性规划问题(nonlinear processing)能有最优化解法的充要条件
- 这部分没有写证明,但是上面的求最值的问题可以被证明是满足KKT条件的问题,所以可以用解决对偶问题的方式来求解。