CS231Nassignment2之FCnet

This part is from the assignment 2018:
stanford cs231n assignment2

目标

• 之前已经实现了两层的fc net，但是在这个网络里面的loss和gradient的计算用的是数学方法
• 这样的计算可以在两层的网络里实现，但是多层的情况下实现起来太困难了
• 所以在这里把电脑分成了forward pass和backward pass

• forward的过程中，接受所有的input，weights，和其他的参数，返回output和cache（存储back的时候需要的东西）

  def layer_forward(x, w):
    """ Receive inputs x and weights w """
    # Do some computations ...
    z = # ... some intermediate value
    # Do some more computations ...
    out = # the output
  
    cache = (x, w, z, out) # Values we need to compute gradients
  
    return out, cache

• back的时候会接受derivative和之前存储的cache，然后计算最后的gradient

  def layer_backward(dout, cache):
    """
    Receive dout (derivative of loss with respect to outputs) and cache,
    and compute derivative with respect to inputs.
    """
    # Unpack cache values
    x, w, z, out = cache
  
    # Use values in cache to compute derivatives
    dx = # Derivative of loss with respect to x
    dw = # Derivative of loss with respect to w
  
    return dx, dw

• 这样就可以组合各个部分达到最终需要的效果了，无论多深都可以实现了

• 还需要一部分的优化部分，包括Dropout，Batch/Layer的Normalization

Affine layer：forward

input

• x：大小（N，d_1…d_k)，minibatch of N，每张图片的维度是d_1到d_k，所以拉成一长条的维度是 d_1 d_2… d_k
• w：weights，(D,M)，把这个长度是d的图片，输出的时候就变成M了
• b:bias,(M,) -> 这个bias会被broadcast到all lines
  • （bias的值是最终分类的class的值，在不是最后一层的时候就是output的值），相当于一个class分一个bias（一列）

output

• output,(N,M)
• cache:(x,w,b)

implement

• 这里的实现直接reshape就可以了，-1的意思是这个维度上不知道有多少反正你自己给我算算的意思，但是需要N行是确定了的
• 注意这里验证的时候虽然input的是size，但是实际上是把数字填到这个里面的，所以取N的时候实际上是x.shape[0]

Affine layer:backward

input

• dout: upstream derivative, shape(N,M)
• cache: Tuple
  • x
  • w
  • b

return

• dx: (N,d1,d2…,dk)
• dw:(D,M)
• db:(M,)

implement

• 注意这里用到的是链式法则：df/dx = df/dq * dq/dx
  • 这里的df/dq就是已经求出来的dout
  • q的式子是 Wx + b，对这三个变量分别求导，求出来大家的，别忘了求导之后的东西需要再乘dout
• 结果到底怎么算应该按每个矩阵的shape来推出来

ReLU activation

forward

• input：x，随便什么尺寸都可以，这部分只是计算relu这个函数
• output
  • out，计算出来的结果
  • cache，储存x，用来back的运算
• implement -> 直接把小于0的部分设置成0就可以了

backward

• input
  • 返回回来的dout
  • cache
• output： 计算出来的x的梯度
• implement:
  • 求导，当原来的x大于0的时候，导数是1，链式法则是dout。小于等于0的时候是dout
  • 所以直接对dout进行操作就可以了

def affine_forward(x, w, b):
    """
    Computes the forward pass for an affine (fully-connected) layer.

    The input x has shape (N, d_1, ..., d_k) and contains a minibatch of N
    examples, where each example x[i] has shape (d_1, ..., d_k). We will
    reshape each input into a vector of dimension D = d_1 * ... * d_k, and
    then transform it to an output vector of dimension M.

    Inputs:
    - x: A numpy array containing input data, of shape (N, d_1, ..., d_k)
    - w: A numpy array of weights, of shape (D, M)
    - b: A numpy array of biases, of shape (M,)

    Returns a tuple of:
    - out: output, of shape (N, M)
    - cache: (x, w, b)
    """
    out = None
    ###########################################################################
    # TODO: Implement the affine forward pass. Store the result in out. You   #
    # will need to reshape the input into rows.                               #
    ###########################################################################
    out = x.reshape(x.shape[0], -1).dot(w) + b

    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = (x, w, b)
    return out, cache


def affine_backward(dout, cache):
    """
    Computes the backward pass for an affine layer.

    Inputs:
    - dout: Upstream derivative, of shape (N, M)
    - cache: Tuple of:
      - x: Input data, of shape (N, d_1, ... d_k)
      - w: Weights, of shape (D, M)
      - b: Biases, of shape (M,)

    Returns a tuple of:
    - dx: Gradient with respect to x, of shape (N, d1, ..., d_k)
    - dw: Gradient with respect to w, of shape (D, M)
    - db: Gradient with respect to b, of shape (M,)
    """
    x, w, b = cache
    dx, dw, db = None, None, None
    ###########################################################################
    # TODO: Implement the affine backward pass.                               #
    ###########################################################################
    dx = dout.dot(w.T).reshape(x.shape)
    dw = (x.reshape(x.shape[0], -1).T).dot(dout)
    db = np.sum(dout, axis=0)
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx, dw, db


def relu_forward(x):
    """
    Computes the forward pass for a layer of rectified linear units (ReLUs).

    Input:
    - x: Inputs, of any shape

    Returns a tuple of:
    - out: Output, of the same shape as x
    - cache: x
    """
    out = None
    ###########################################################################
    # TODO: Implement the ReLU forward pass.                                  #
    ###########################################################################
    out = x.copy()
    out[out <= 0] = 0.0
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = x
    return out, cache


def relu_backward(dout, cache):
    """
    Computes the backward pass for a layer of rectified linear units (ReLUs).

    Input:
    - dout: Upstream derivatives, of any shape
    - cache: Input x, of same shape as dout

    Returns:
    - dx: Gradient with respect to x
    """
    dx, x = None, cache
    ###########################################################################
    # TODO: Implement the ReLU backward pass.                                 #
    ###########################################################################
    dout[x <= 0] = 0
    dx = dout
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx

sandwich layer

在文件cs231n/layer_utils.py里面，有一些比较常见的组合，可以集成成新的函数，这样用的时候就可以直接调用不用自己写了

loss layer -> 和assignment1里面写的内容是一样的

two-layer network

cs231n/classifiers/fc_net.py TwoLayerNet

init__

• 需要初始化weights和bias，weights应该是0.0中心的高斯（=weight_scale），bias应该是0，都存在self.para的字典里面，第几层的名字就叫第几
• input
  • 图片的size
  • hidden的个数
  • class的数量
  • weight scale，看初始的weights怎么分布
  • reg，regularization时候的权重

forward

• 用前面已经写好的东西计算前向
• 最后得到scores
• 再用scores计算loss，注意 计算loss也是一层
• 计算loss的时候注意他这里loss的参数是scores和lable

backward

• back的时候不要忘记了loss也是一层，所以输入第二个sandwich的时候输入的应该是dscores而不是scores？！！！！
• 计算gradient，注意他的function里面已经除了总数！
• 别忘了加上L2的regularization

Solver

把之前那些训练啊，验证啊，计算accuracy之类的部分全都扔到一个class里面叫做solver，打开cs231n/solver.py

作用

• solver部分包括所有训练分类所需要的逻辑部分，在optim.py里面还用了不同的update方法来实现SGD
• 这个class接受training和validation的数据和labels，所以可以检查分类的准确率，是否overfitting
• 需要先构成一个solver的instance，把需要的model，dataset，和不同的东西（learning rate，batch，etc）放进去
• 先用train()来训练，然后model的para都存着所有训练完的参数
• 训练的过程也会记录下来（accuracy的改变啥的）

最后训练的结果大约在50%

model = TwoLayerNet()
solver = None

##############################################################################
# TODO: Use a Solver instance to train a TwoLayerNet that achieves at least  #
# 50% accuracy on the validation set.                                        #
##############################################################################

solver = Solver(model, data, 
                update_rule = 'sgd',
                optim_config={'learning_rate': 1e-3,},
                lr_decay=0.95,
                num_epochs=10, batch_size=100,
                print_every=100)

solver.train()
##############################################################################
#                             END OF YOUR CODE                               #
#######################################################################

可视化这个最终的结果，loss随着epoch的变化和training acc以及val acc的变化

# Run this cell to visualize training loss and train / val accuracy

plt.subplot(2, 1, 1)
plt.title('Training loss')
plt.plot(solver.loss_history, 'o')
plt.xlabel('Iteration')

plt.subplot(2, 1, 2)
plt.title('Accuracy')
plt.plot(solver.train_acc_history, '-o', label='train')
plt.plot(solver.val_acc_history, '-o', label='val')
plt.plot([0.5] * len(solver.val_acc_history), 'k--')
plt.xlabel('Epoch')
plt.legend(loc='lower right')
plt.gcf().set_size_inches(15, 12)
plt.show()

记下来了这个loss和acc的history，所以就可以直接用来可视化了！

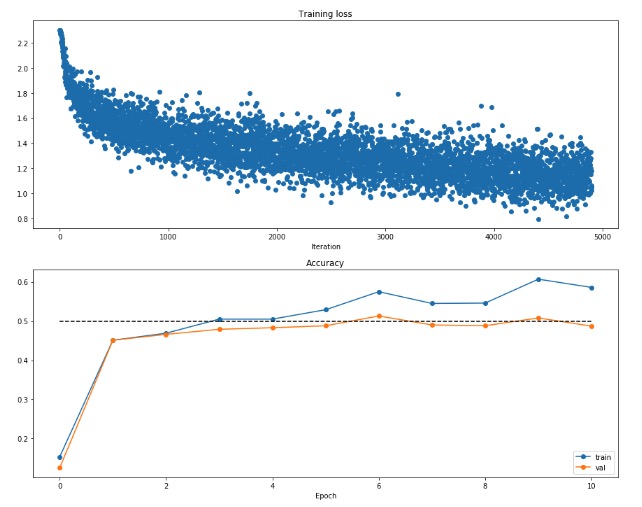
Multilayer network

现在开始实现有多层的net

• 需要注意的问题主要是数数数对了，注意数字和layer的数量的关系
• 为了保证验证的准确，需要把loss的regularization算对才可以
• 反向往回推的时候，可以用 reversed(range(a))这个东西来进行
• 总体来说和两层的差不多，就是加进来了for循环

class FullyConnectedNet(object):
    """
    A fully-connected neural network with an arbitrary number of hidden layers,
    ReLU nonlinearities, and a softmax loss function. This will also implement
    dropout and batch/layer normalization as options. For a network with L layers,
    the architecture will be

    {affine - [batch/layer norm] - relu - [dropout]} x (L - 1) - affine - softmax

    where batch/layer normalization and dropout are optional, and the {...} block is
    repeated L - 1 times.

    Similar to the TwoLayerNet above, learnable parameters are stored in the
    self.params dictionary and will be learned using the Solver class.
    """

    def __init__(self, hidden_dims, input_dim=3 * 32 * 32, num_classes=10,
                 dropout=1, normalization=None, reg=0.0,
                 weight_scale=1e-2, dtype=np.float32, seed=None):
        """
        Initialize a new FullyConnectedNet.

        Inputs:
        - hidden_dims: A list of integers giving the size of each hidden layer.
        - input_dim: An integer giving the size of the input.
        - num_classes: An integer giving the number of classes to classify.
        - dropout: Scalar between 0 and 1 giving dropout strength. If dropout=1 then
          the network should not use dropout at all.
        - normalization: What type of normalization the network should use. Valid values
          are "batchnorm", "layernorm", or None for no normalization (the default).
        - reg: Scalar giving L2 regularization strength.
        - weight_scale: Scalar giving the standard deviation for random
          initialization of the weights.
        - dtype: A numpy datatype object; all computations will be performed using
          this datatype. float32 is faster but less accurate, so you should use
          float64 for numeric gradient checking.
        - seed: If not None, then pass this random seed to the dropout layers. This
          will make the dropout layers deteriminstic so we can gradient check the
          model.
        """
        self.normalization = normalization
        self.use_dropout = dropout != 1
        self.reg = reg
        self.num_layers = 1 + len(hidden_dims)
        self.dtype = dtype
        self.params = {}

        ############################################################################
        # TODO: Initialize the parameters of the network, storing all values in    #
        # the self.params dictionary. Store weights and biases for the first layer #
        # in W1 and b1; for the second layer use W2 and b2, etc. Weights should be #
        # initialized from a normal distribution centered at 0 with standard       #
        # deviation equal to weight_scale. Biases should be initialized to zero.   #
        #                                                                          #
        # When using batch normalization, store scale and shift parameters for the #
        # first layer in gamma1 and beta1; for the second layer use gamma2 and     #
        # beta2, etc. Scale parameters should be initialized to ones and shift     #
        # parameters should be initialized to zeros.                               #
        ############################################################################
        pr_num = input_dim

        # can't use enumerate beacuse I need the number more than the size of hidden_dims
        for layer in range(self.num_layers):
            layer += 1
            weights = 'W' + str(layer)
            bias = 'b' + str(layer)

            # 这时候是最后一层(the last layer)
            if layer == self.num_layers:
                self.params[weights] = np.random.randn(
                    hidden_dims[len(hidden_dims) - 1], num_classes) * weight_scale
                self.params[bias] = np.zeros(num_classes)

            # other layers
            else:
                hidd_num = hidden_dims[layer - 1]
                self.params[weights] = np.random.randn(
                    pr_num, hidd_num) * weight_scale
                self.params[bias] = np.zeros(hidd_num)
                pr_num = hidd_num

            if self.normalization in ["batchnorm", "layernorm"]:
                self.params['gamma' + str(layer)] = np.ones(hidd_num)
                self.params['bata' + str(layer)] = np.zeros(hidd_num)

        # print(len(self.params))
        # print(self.params)
        ############################################################################
        #                             END OF YOUR CODE                             #
        ############################################################################

        # When using dropout we need to pass a dropout_param dictionary to each
        # dropout layer so that the layer knows the dropout probability and the mode
        # (train / test). You can pass the same dropout_param to each dropout layer.
        self.dropout_param = {}
        if self.use_dropout:
            self.dropout_param = {'mode': 'train', 'p': dropout}
            if seed is not None:
                self.dropout_param['seed'] = seed

        # With batch normalization we need to keep track of running means and
        # variances, so we need to pass a special bn_param object to each batch
        # normalization layer. You should pass self.bn_params[0] to the forward pass
        # of the first batch normalization layer, self.bn_params[1] to the forward
        # pass of the second batch normalization layer, etc.
        self.bn_params = []
        if self.normalization == 'batchnorm':
            self.bn_params = [{'mode': 'train'}
                              for i in range(self.num_layers - 1)]
        if self.normalization == 'layernorm':
            self.bn_params = [{} for i in range(self.num_layers - 1)]

        # Cast all parameters to the correct datatype
        for k, v in self.params.items():
            self.params[k] = v.astype(dtype)

    def loss(self, X, y=None):
        """
        Compute loss and gradient for the fully-connected net.

        Input / output: Same as TwoLayerNet above.
        """
        X = X.astype(self.dtype)
        mode = 'test' if y is None else 'train'

        # Set train/test mode for batchnorm params and dropout param since they
        # behave differently during training and testing.
        if self.use_dropout:
            self.dropout_param['mode'] = mode
        if self.normalization == 'batchnorm':
            for bn_param in self.bn_params:
                bn_param['mode'] = mode
        scores = None
        ############################################################################
        # TODO: Implement the forward pass for the fully-connected net, computing  #
        # the class scores for X and storing them in the scores variable.          #
        #                                                                          #
        # When using dropout, you'll need to pass self.dropout_param to each       #
        # dropout forward pass.                                                    #
        #                                                                          #
        # When using batch normalization, you'll need to pass self.bn_params[0] to #
        # the forward pass for the first batch normalization layer, pass           #
        # self.bn_params[1] to the forward pass for the second batch normalization #
        # layer, etc.                                                              #
        ############################################################################
        cache = {}
        temp_out = X
        for i in range(self.num_layers):
            w = self.params['W' + str(i + 1)]
            b = self.params['b' + str(i + 1)]
            if i == self.num_layers - 1:
                scores, cache['cache' +
                              str(i + 1)] = affine_relu_forward(temp_out, w, b)
            else:
                temp_out, cache['cache' +
                                str(i + 1)] = affine_relu_forward(temp_out, w, b)

        ############################################################################
        #                             END OF YOUR CODE                             #
        ############################################################################

        # If test mode return early
        if mode == 'test':
            return scores

        loss, grads = 0.0, {}
        ############################################################################
        # TODO: Implement the backward pass for the fully-connected net. Store the #
        # loss in the loss variable and gradients in the grads dictionary. Compute #
        # data loss using softmax, and make sure that grads[k] holds the gradients #
        # for self.params[k]. Don't forget to add L2 regularization!               #
        #                                                                          #
        # When using batch/layer normalization, you don't need to regularize the scale   #
        # and shift parameters.                                                    #
        #                                                                          #
        # NOTE: To ensure that your implementation matches ours and you pass the   #
        # automated tests, make sure that your L2 regularization includes a factor #
        # of 0.5 to simplify the expression for the gradient.                      #
        ############################################################################
        loss, dscores = softmax_loss(scores, y)
        reg_loss = 0.0
        pre_dx = dscores

        for i in reversed(range(self.num_layers)):
            i = i + 1

            reg_loss = np.sum(np.square(self.params['W' + str(i)]))
            loss += reg_loss * 0.5 * self.reg

            pre_dx, dw, db = affine_relu_backward(
                pre_dx, cache['cache' + str(i)])
            dw += self.reg * self.params['W' + str(i)]
            db += self.reg * self.params['b' + str(i)]

            grads['W' + str(i)] = dw
            grads['b' + str(i)] = db

        ############################################################################
        #                             END OF YOUR CODE                             #
        ############################################################################

        return loss, grads

检测网络是否overfitting

• 选择了一个三层的网络，小幅度改变learning rate和init scale
• 尝试去overfitting
  出现了一些问题不是太能overfitting我不知道为什么

update rules

在得到了back出来的dw之后，就需要用这个dw对w进行update，这里有一些比较常见的update方法

普通的update

• 仅仅沿着gradient改变的反方向进行(反方向是因为计算出来的gradient是上升的方向)
  x += - learning_rate * dx

SGD + momentum

http://cs231n.github.io/neural-networks-3/#sgd

• 是对这个update一点物理上比较直观的理解（其实名字叫做动量）

  • 可以理解为这个东西是在一个平原上跑的一个球，我们需要求的w是这个球的速度，得到的dw是这个球的加速度，而这个球的初速度是0
  • 可以理解为这个球找最低点的时候，除了每步按dw update，还在上面加上了前面速度的影响，也就是加上了惯性！

    # Momentum update
    v = mu * v - learning_rate * dx # integrate velocity
    x += v # integrate position

• Nesterov Momentum(NAG)

  • 在原来的基础上：真实移动方向 = 速度的影响（momentum）+ 梯度的影响 （gradient）
  • 现在：既然我们已经知道了要往前走到动量的影响的位置，那么我根据那个位置的梯度再进行update，岂不是跑的更快！
  • 总的来说就是考虑到了前面的坡度（二阶导数），如果前面的坡度缓的话我就再跑快点，如果陡的话就跑慢点

    v_prev = v # back this up
    v = mu * v - learning_rate * dx # velocity update stays the same
    x += -mu * v_prev + (1 + mu) * v # position update changes form

cs231n/optim.py

• 加入了新的计算update的方法
• 具体的原理还没有看，但是计算就是这样计算的

def sgd_momentum(w, dw, config=None):
    """
    Performs stochastic gradient descent with momentum.

    config format:
    - learning_rate: Scalar learning rate.
    - momentum: Scalar between 0 and 1 giving the momentum value.
      Setting momentum = 0 reduces to sgd.
    - velocity: A numpy array of the same shape as w and dw used to store a
      moving average of the gradients.
    """
    if config is None:
        config = {}
    config.setdefault('learning_rate', 1e-2)
    config.setdefault('momentum', 0.9)
    v = config.get('velocity', np.zeros_like(w))

    next_w = None
    ###########################################################################
    # TODO: Implement the momentum update formula. Store the updated value in #
    # the next_w variable. You should also use and update the velocity v.     #
    ###########################################################################
    v = config['momentum'] * v - config['learning_rate'] * dw
    w += v
    next_w = w
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    config['velocity'] = v

    return next_w, config

• 可以看出来最终的结果会比普通的SGD上升的更快
  

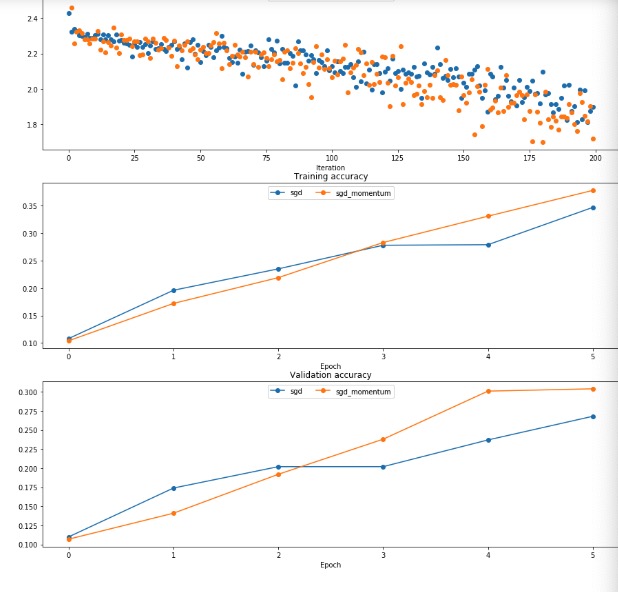
分别又尝试了RMSProp and Adam