CS231Nassignment2之Batch Normalization

target

之前的内容讲了lr的优化方法，比如Adam，另一种方法是根据改变网络的结构，make it easy to train -> batch normalization
想去掉一些uncorrelated features(不相关的特征)，可以在训练数据之前preprocess，变成0-centered分布，这样第一层是没有问题的，但是后面的层里还是会出问题
所以把normalization的部分加入了DN里面，加入了一个BN层，会估计mean和standard deviation of each feature，这样重新centre和normalized
learnable shift and scale parameters for each feature dimension
核心思想：粗暴的用BN来解决weights初始化的问题

ref：https://kratzert.github.io/2016/02/12/understanding-the-gradient-flow-through-the-batch-normalization-layer.html

Batch normalization: forward

这个东西的要义就是NN里面的一层，不对维度改变，但是会改变这些值的分布

首先setup，并且载入好了preprocess的数据
cs231n/layers.py -> batchnorm_forward

keep exp decay 来运行mean & variance of each feature -> 在test的时候去normalize data
test-time: 计算sample mean和varience的时候用大量的训练数据而不是用所有图片的平均值，但是在作业里面用的是平均值，因为可以省去一步estimate（torch7 也用的是平均值）

1 2	running_mean = momentum * running_mean + (1 - momentum) * sample_mean running_var = momentum * running_var + (1 - momentum) * sample_var

I/O

input
- x，data(N,D)
- gamma：scale parameter(D,)
- beta：shift parameter(D,)
- bn_param: 一个dict
  - mode：‘train’ or ‘test’
  - eps：为了数字上的稳定性的一个常数
  - momentum：在计算mean和variance上面的一个常数
  - running mean：(D,)，是running mean
  - running var：(D,)
output
- out：(N,D)
- cache:在back的时候用

todo

用minibatch的统计来计算mean和variance，用这两个值把data normalize，并且用gamma和beta拉伸这个值，以及shift这些值的位置
在分布的上面，虽然求得是running variance，但是需要normalize的时候考虑的是standard（也就是平方根）

implement

其实是和如何计算息息相关的，知道输入，求这个玩意的normal的步骤如下（其中的x就是这个minibatch的全部数据）
- 求mu，也就是x的mean（注意这里要对列求mean，也就是把所有图片的像素均匀分布，最后得到的结果是D个不是N个）
- 求var，知道这个东西，可以直接用 np.var(x, axis = 0)来求方差
- 求normalize： x - x.mean / np.sqrt(x.var + eps)
  - 其中刚开始求出来的var就是方差，也就是标准差的平方
  - eps是偏差值，这个值加上方差开方是标准差
- scale和shift，乘scale的系数，加shift的系数
最后需要计算什么cache和back的推导息息相关

Batch normalization: backward

可以直接画出来计算normal的路径，然后根据这个路径back
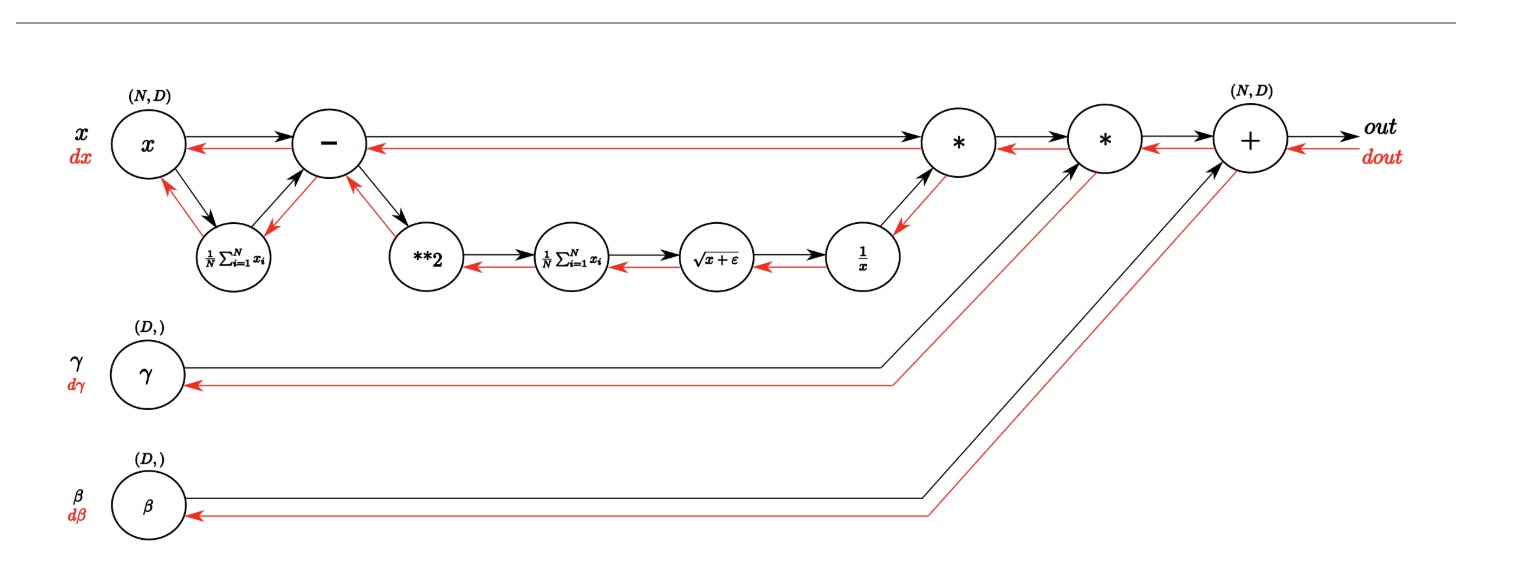
要义就是一步一步的求导！一步一步的链式法则
注意的就是求mean回来的导数，理解上来说就是这个矩阵在求导的过程中升维了，从(D,)变成了(N,D)，而在最开始求得时候所有的数字的贡献都是1，所以往回走的时候乘一个（N，D）的全是1的矩阵，并且1/N的常数还在

Batch normalization: alternative backward

在sigmoid的back的过程中有两种不同的方法
- 一种是写出来整体计算的图（拆分成各种小的计算），然后根据这张图的再back回去
- 另一种是在纸上先简化了整体的计算过程，然后再直接实现，这样代码会比较简单
ref:https://kevinzakka.github.io/2016/09/14/batch_normalization/

最终目标

f: BN之后的整体输出结果
y：对normal之后的线性变换（gamma + beta）
x’：normal的input
mu：batch mean
varbatch vatiance
需要求 df/dx,df/dgamma,df/dbeta -> 最终结果整体速度比以前快了x2.5左右，这一步的主要目的就是用来提速的

可以把整体的计算分为以下的三个步骤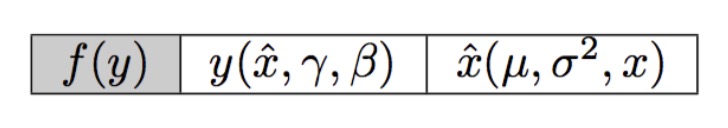

这三部分的代码如下

def batchnorm_forward(x, gamma, beta, bn_param):
    """
    Forward pass for batch normalization.

    During training the sample mean and (uncorrected) sample variance are
    computed from minibatch statistics and used to normalize the incoming data.
    During training we also keep an exponentially decaying running mean of the
    mean and variance of each feature, and these averages are used to normalize
    data at test-time.

    At each timestep we update the running averages for mean and variance using
    an exponential decay based on the momentum parameter:

    running_mean = momentum * running_mean + (1 - momentum) * sample_mean
    running_var = momentum * running_var + (1 - momentum) * sample_var

    Note that the batch normalization paper suggests a different test-time
    behavior: they compute sample mean and variance for each feature using a
    large number of training images rather than using a running average. For
    this implementation we have chosen to use running averages instead since
    they do not require an additional estimation step; the torch7
    implementation of batch normalization also uses running averages.

    Input:
    - x: Data of shape (N, D)
    - gamma: Scale parameter of shape (D,)
    - beta: Shift paremeter of shape (D,)
    - bn_param: Dictionary with the following keys:
      - mode: 'train' or 'test'; required
      - eps: Constant for numeric stability
      - momentum: Constant for running mean / variance.
      - running_mean: Array of shape (D,) giving running mean of features
      - running_var Array of shape (D,) giving running variance of features

    Returns a tuple of:
    - out: of shape (N, D)
    - cache: A tuple of values needed in the backward pass
    """
    mode = bn_param['mode']
    eps = bn_param.get('eps', 1e-5)
    momentum = bn_param.get('momentum', 0.9)

    N, D = x.shape
    running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
    running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))

    out, cache = None, None
    if mode == 'train':
        #######################################################################
        # TODO: Implement the training-time forward pass for batch norm.      #
        # Use minibatch statistics to compute the mean and variance, use      #
        # these statistics to normalize the incoming data, and scale and      #
        # shift the normalized data using gamma and beta.                     #
        #                                                                     #
        # You should store the output in the variable out. Any intermediates  #
        # that you need for the backward pass should be stored in the cache   #
        # variable.                                                           #
        #                                                                     #
        # You should also use your computed sample mean and variance together #
        # with the momentum variable to update the running mean and running   #
        # variance, storing your result in the running_mean and running_var   #
        # variables.                                                          #
        #                                                                     #
        # Note that though you should be keeping track of the running         #
        # variance, you should normalize the data based on the standard       #
        # deviation (square root of variance) instead!                        #
        # Referencing the original paper (https://arxiv.org/abs/1502.03167)   #
        # might prove to be helpful.                                          #
        #######################################################################
        mean = np.mean(x, axis=0)
        xmu = x - mean
        sq = np.square(xmu)
        var = np.var(x, axis=0)
        sqrtvar = np.sqrt(var + eps)
        ivar = 1. / sqrtvar
        normalize_raw = xmu * ivar

        normalize_result = gamma * normalize_raw + beta
        out = normalize_result

        running_mean = momentum * running_mean + \
            (1 - momentum) * mean
        running_var = momentum * running_var + (1 - momentum) * var

        cache = (normalize_raw, gamma, xmu, ivar, sqrtvar, var, eps)
        #######################################################################
        #                           END OF YOUR CODE                          #
        #######################################################################
    elif mode == 'test':
        #######################################################################
        # TODO: Implement the test-time forward pass for batch normalization. #
        # Use the running mean and variance to normalize the incoming data,   #
        # then scale and shift the normalized data using gamma and beta.      #
        # Store the result in the out variable.                               #
        #######################################################################
        x_normalize = (x - running_mean) / (np.sqrt(running_var + eps))
        out = x_normalize * gamma + beta
        #######################################################################
        #                          END OF YOUR CODE                           #
        #######################################################################
    else:
        raise ValueError('Invalid forward batchnorm mode "%s"' % mode)

    # Store the updated running means back into bn_param
    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var

    return out, cache


def batchnorm_backward(dout, cache):
    """
    Backward pass for batch normalization.

    For this implementation, you should write out a computation graph for
    batch normalization on paper and propagate gradients backward through
    intermediate nodes.

    Inputs:
    - dout: Upstream derivatives, of shape (N, D)
    - cache: Variable of intermediates from batchnorm_forward.

    Returns a tuple of:
    - dx: Gradient with respect to inputs x, of shape (N, D)
    - dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
    - dbeta: Gradient with respect to shift parameter beta, of shape (D,)
    """
    dx, dgamma, dbeta = None, None, None
    ###########################################################################
    # TODO: Implement the backward pass for batch normalization. Store the    #
    # results in the dx, dgamma, and dbeta variables.                         #
    # Referencing the original paper (https://arxiv.org/abs/1502.03167)       #
    # might prove to be helpful.                                              #
    ###########################################################################
    normalize_raw, gamma, xmu, ivar, sqrtvar, var, eps = cache
    N, D = dout.shape

    dbeta = np.sum(dout, axis=0)
    dgammax = dout

    dgamma = np.sum(dgammax * normalize_raw, axis=0)
    dnormalize_raw = dgammax * gamma

    divar = np.sum(dnormalize_raw * xmu, axis=0)
    dxmu = dnormalize_raw * ivar

    dsqrtvar = -1. / (sqrtvar ** 2) * divar

    dvar = 0.5 * 1. / np.sqrt(var + eps) * dsqrtvar

    dsq = 1. / N * np.ones((N, D)) * dvar

    dxmu2 = 2 * xmu * dsq

    dx1 = (dxmu + dxmu2)
    dmu = -1 * np.sum(dxmu + dxmu2, axis=0)

    dx2 = 1. / N * np.ones((N, D)) * dmu

    dx = dx1 + dx2
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################

    return dx, dgamma, dbeta


def batchnorm_backward_alt(dout, cache):
    """
    Alternative backward pass for batch normalization.

    For this implementation you should work out the derivatives for the batch
    normalizaton backward pass on paper and simplify as much as possible. You
    should be able to derive a simple expression for the backward pass. 
    See the jupyter notebook for more hints.

    Note: This implementation should expect to receive the same cache variable
    as batchnorm_backward, but might not use all of the values in the cache.

    Inputs / outputs: Same as batchnorm_backward
    """
    dx, dgamma, dbeta = None, None, None
    ###########################################################################
    # TODO: Implement the backward pass for batch normalization. Store the    #
    # results in the dx, dgamma, and dbeta variables.                         #
    #                                                                         #
    # After computing the gradient with respect to the centered inputs, you   #
    # should be able to compute gradients with respect to the inputs in a     #
    # single statement; our implementation fits on a single 80-character line.#
    ###########################################################################
    normalize_raw, gamma, xmu, ivar, sqrtvar, var, eps = cache
    N, D = dout.shape

    dbeta = np.sum(dout, axis=0)
    dgamma = np.sum(dout * normalize_raw, axis=0)

    # intermediate partial derivatives
    dxhat = dout * gamma

    # final partial derivatives
    dx = (1. / N) * ivar * (N * dxhat - np.sum(dxhat, axis=0)
                            - normalize_raw * np.sum(dxhat * normalize_raw, axis=0))

    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################

    return dx, dgamma, dbeta

Fully Connected Nets with Batch Normalization

in cs231n/classifiers/fc_net.py, add the BN layers into the net.

应该在每个relu之前加上BN，所以在这里不能直接用之前的affine，relu的过程，因为中间又插了一个新的BN层，所以要写一个新的function
最后一层之后的输出不应该BN(应该是涉及到循环的问题)

实现中遇到的问题

self.bn_params的参数类型不是dict而是list，代表的是所有层里面的参数的所有和，当进入到每层的时候具体对应的才是这里的dict
当把affine_BN_relu结合在一起的时候，注意最后一层输出的地方没有BN，所以没有他的cache，需要分开讨论，不然cache的数量不对
注意这个fc_net的class因为需要实现多种不同的功能，所以对于是不是BN要加上条件判断
确实非常像搭乐高了！！
这里主要，写到这才发现最后一层的时候好像是不需要relu也不需要batchnorm

定义好的函数块

def affine_BN_relu_forward(self, x, w, b, gamma, beta, bn_params):
       a, fc_cache = affine_forward(x, w, b)
       mid, BN_cache = batchnorm_forward(a, gamma, beta, bn_params)
       out, relu_cache = relu_forward(mid)
       cache = (fc_cache, BN_cache, relu_cache)

       return out, cache

   def affine_BN_relu_backward(self, dout, cache):
       fc_cache, BN_cache, relu_cache = cache
       da = relu_backward(dout, relu_cache)
       dmin, dgamma, dbeta = batchnorm_backward_alt(da, BN_cache)
       dx, dw, db = affine_backward(dmin, fc_cache)

       return dx, dw, db, dgamma, dbeta

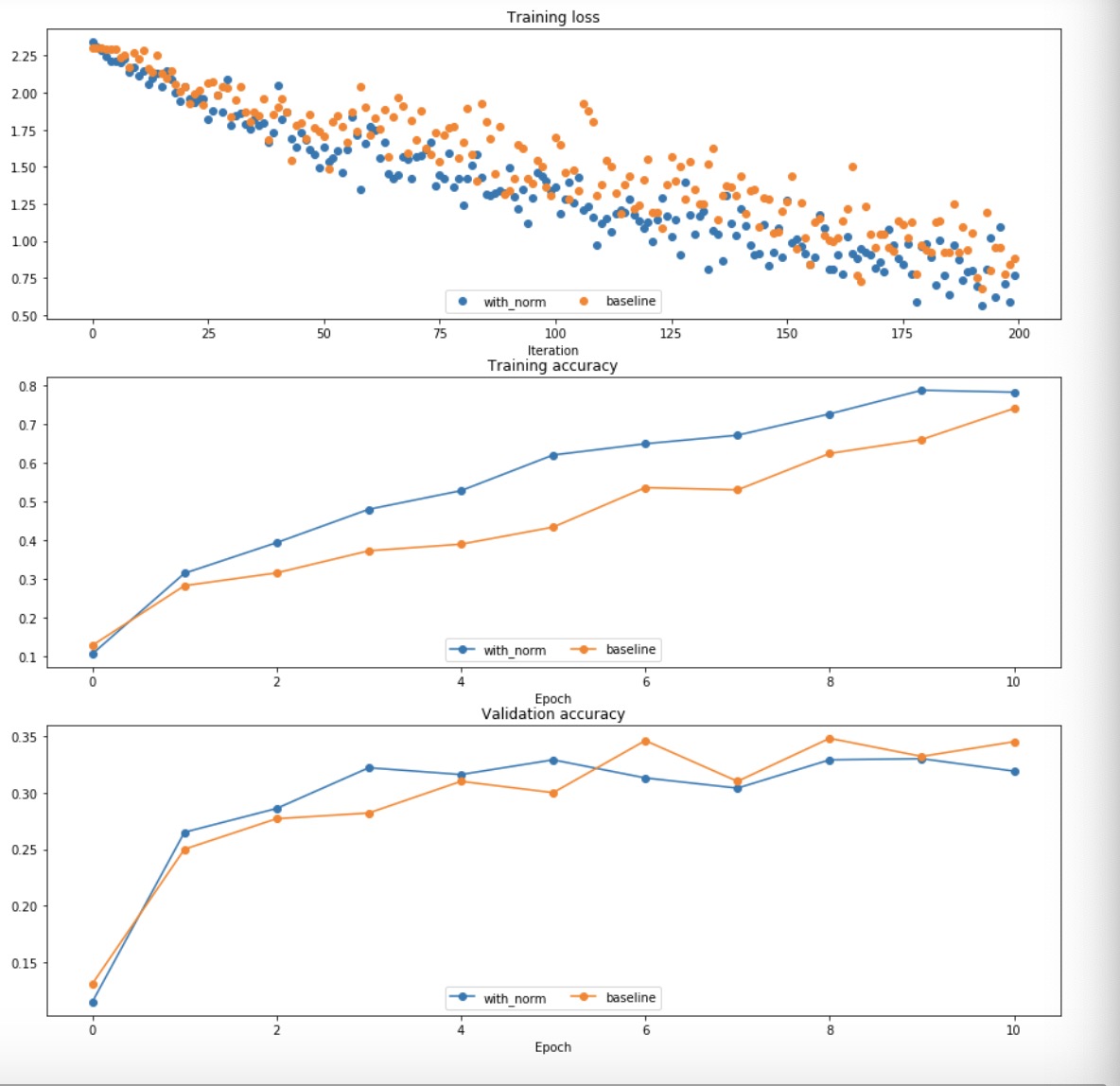
结论

可视化之后可以发现加了norm的话好像会下降的快一点

Batch normalization and initialization

进行试验，了解BN和weight initialization的关系
训练一个八层的网络，包括和不包括BN，用不同的weight initialization
plot出来train acc, val_acc,train_loss和weight initialization的关系

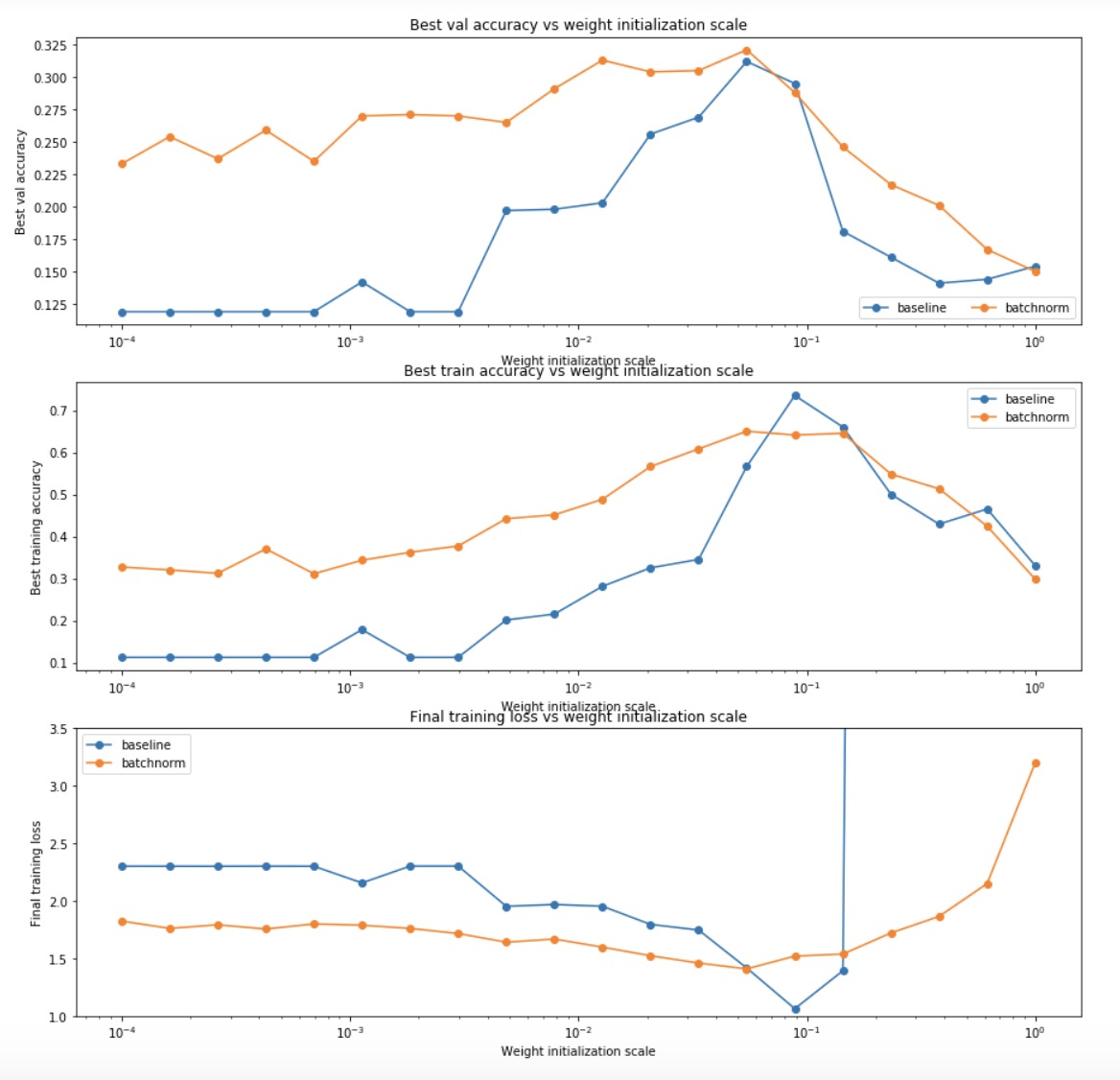
image_5vis

BN的作用

从图中可以看出来，有了BN以后，weight init对最终结果的影响明显会降低：

weight的初始化对最终结果影响很严重，比如如果全是0的话，得到的所有neuron的功能都是一样的
BN其实就是在实际中解决weight init的办法，这样可以减少初始化参数的影响
- 核心思想就是如果你需要更好的分布，你就加一层让他变成更好的分布
- 在计算的过程中越乘越小（或者越大），所以计算出来的结果越来越接近0
- 所以这时候如果把一些input重新分布了，就会减少这个接近0的可能性

Batch normalization and batch size

试验验证BN和batch size的关系
训练6-layer的网络，分别with和without BN，使用不同的batch size

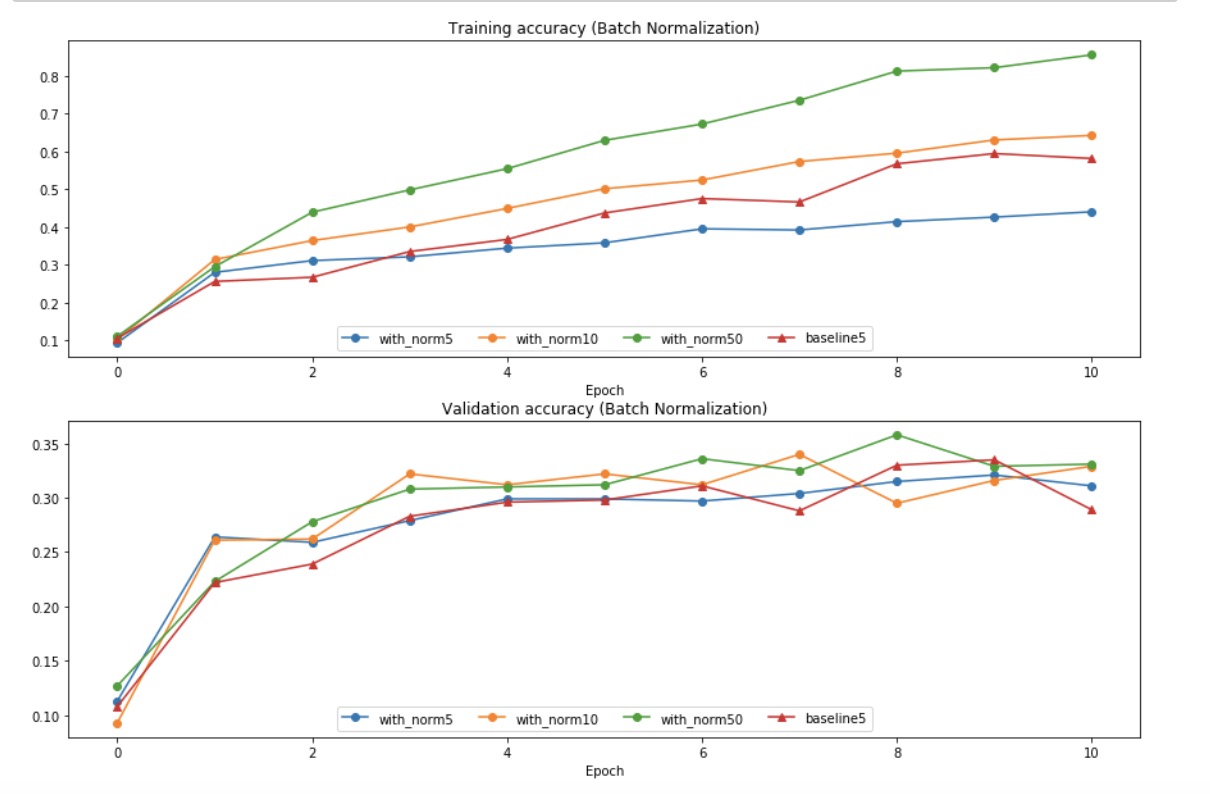
image_6vis

By increasing batch size your steps can be more accurate because your sampling will be closer to the real population. If you increase the size of batch, your batch normalisation can have better results. The reason is exactly like the input layer. The samples will be closer to the population for inner activations.

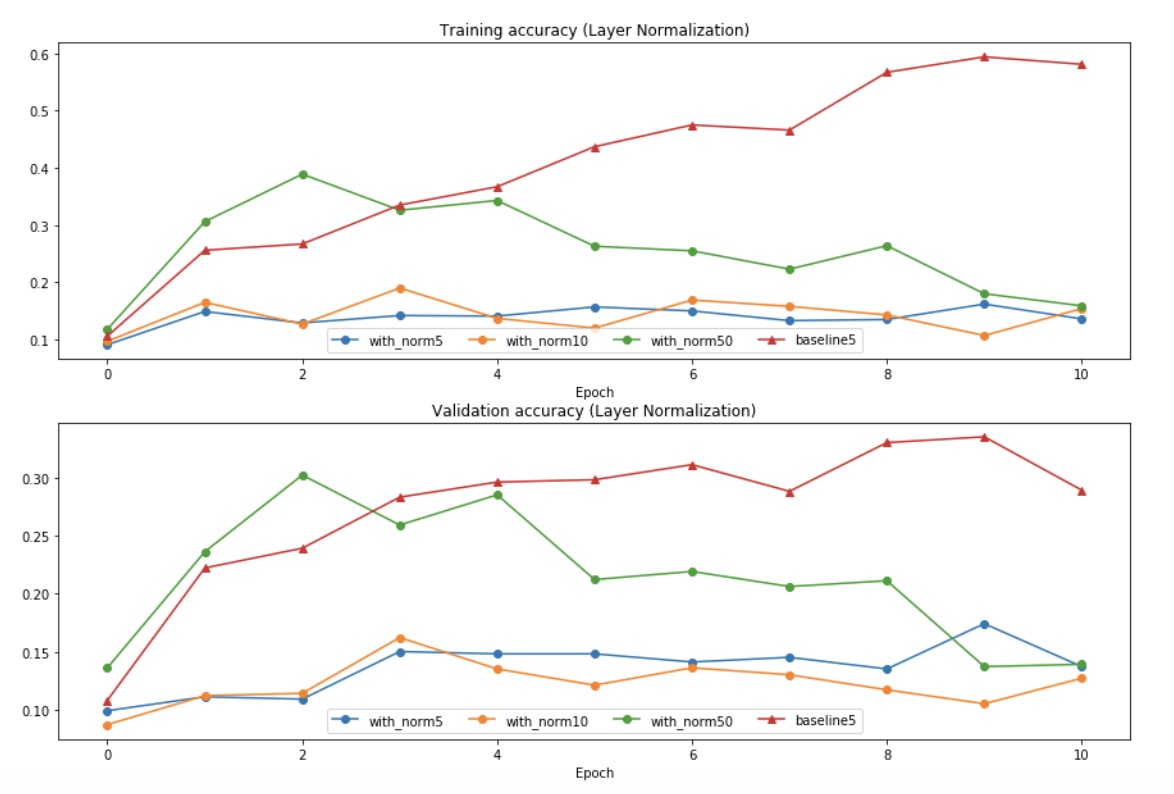
Layer Normalization（LN）

前面的所有的BN已经可以让Net更好的被训练了，但是BN的大小和batch的大小有关，所以在实际应用的时候会受到一些限制
- 在复杂的网络里面的时候，batch_size是被硬件机能限制的
- 每个minibatch的数据分布可能会比较接近，所以训练之前要shuffle，否则结果会差很多
其中一种解决的方法就是layer normalization
- 不是在batch上面normal
- 在layer上面normal
- each feature vector corresponding to a single datapoint is normalized based on the sum of all terms within that feature vector.
Ba, Jimmy Lei, Jamie Ryan Kiros, and Geoffrey E. Hinton. “Layer Normalization.” stat 1050 (2016): 21.

LN

综合一层的所有维度的输入，计算该层的平均输入和平均方差
然后用同一个规范化操作转换各个维度的输入
相当于以前我们希望可以正则到这个minibatch里面的大家都差不多，现在我们不管batch了，而是调整到一张图片里面的所有数据都是normal的

implement

cs231n/layers.py -> layernorm_backward

forward + back

input
- x, (N,D)
- gamma, scale
- beta,shift
- ln_params: eps
output
- output,(N,D)
- cache
实现方法 -> 实际上就是从对一列的操作变成了对一行的操作
- 比如之前对x取mean就是求每列的mean，现在变成了取每行的mean
- 在所有normal之后并且scale之前，把这个矩阵在tranpose回来
back
- 把需要参与计算的东西都tranpose
- 然后把计算完的dx tranpose回来

fc_nets

在fc_nets里面稍加改动，在normalization里面增加BN_NORM和Layer_NORM的选项就可以了，整体改动不大

def affine_Normal_relu_forward(self, x, w, b, gamma, beta, bn_params, mode):
      a, fc_cache = affine_forward(x, w, b)
      if mode == "batchnorm":
          mid, Normal_cache = batchnorm_forward(a, gamma, beta, bn_params)
      elif mode == "layernorm":
          mid, Normal_cache = layernorm_forward(a, gamma, beta, bn_params)
      out, relu_cache = relu_forward(mid)
      cache = (fc_cache, Normal_cache, relu_cache)

      return out, cache

  def affine_Normal_relu_backward(self, dout, cache, mode):
      fc_cache, Normal_cache, relu_cache = cache
      da = relu_backward(dout, relu_cache)
      if mode == "batchnorm":
          dmid, dgamma, dbeta = batchnorm_backward_alt(da, Normal_cache)
      elif mode == "layernorm":
          dmid, dgamma, dbeta = layernorm_backward(da, Normal_cache)
      dx, dw, db = affine_backward(dmid, fc_cache)

      return dx, dw, db, dgamma, dbeta

可以从图像看出来，layernorm中，batchsize的影响变小了
image_7vis