CS231nassignment2CNN

target

之前已经实践了fc的相关东西，但是在实际的使用里大家使用的都是CNN
所以这部分就开始实践CNN了

convolution: Native forward pass

CNN的核心部分就是卷积
in cs231n/layers.py，conv_forward_naive
首先这时候不用考虑效率问题，最轻松的写就可以了
输入的数据是N个data，每个有C个channel，H的高度和W的宽度
每个输入和F个不同的filter做卷积，每个卷积核对所有的channel作用，卷积核的大小是HHxWW

input

x, (N,C,H,W)
w, fliter weights of shape (F,C,HH,WW)
b, bias, (F,)
conv_param: dict
- “stride” 步长
- “pad” zero-padding的大小

注意在padding的时候不要调整x，而是得到一个padding之后的新的东西

output

out, (N,F,H’,W’)
- H’ = 1 + (H + 2 * pad - HH) / stride
- W’ = 1 + (W + 2 * pad - WW) / stride
cache: (x,w,b,conv_param)

implement

首先需要对输入的图片进行padding
- np.pad
  - 输入的array
  - pad的宽度，如果默认的话就是前后都加，然后是这个数字的宽度 -> 注意这里的时候因为一共有四个维度，前两个维度是不用pad的
  - mode = ‘constant’
  - constant_values，表示的是pad进去的值，可以前后pad的不一样，因为这里是0-padding所以这里是0
要对所有图片进行处理，需要在N个图片里选择一个
在filter的所有里面选择一个
考虑在H方向和W方向的移动步数，然后通过这个步数和步长的乘积在原图里面取需要做卷积的部分
- 注意这里可以不用考虑channel，因为图片和filter的channel是同样的层数，所以直接可以boardcast
然后这个部分和卷积核相乘（直接乘），求和，加上bias，就是这个像素点上应该的数值

def conv_forward_naive(x, w, b, conv_param):
    """
    A naive implementation of the forward pass for a convolutional layer.

    The input consists of N data points, each with C channels, height H and
    width W. We convolve each input with F different filters, where each filter
    spans all C channels and has height HH and width WW.

    Input:
    - x: Input data of shape (N, C, H, W)
    - w: Filter weights of shape (F, C, HH, WW)
    - b: Biases, of shape (F,)
    - conv_param: A dictionary with the following keys:
      - 'stride': The number of pixels between adjacent receptive fields in the
        horizontal and vertical directions.
      - 'pad': The number of pixels that will be used to zero-pad the input.


    During padding, 'pad' zeros should be placed symmetrically (i.e equally on both sides)
    along the height and width axes of the input. Be careful not to modfiy the original
    input x directly.

    Returns a tuple of:
    - out: Output data, of shape (N, F, H', W') where H' and W' are given by
      H' = 1 + (H + 2 * pad - HH) / stride
      W' = 1 + (W + 2 * pad - WW) / stride
    - cache: (x, w, b, conv_param)
    """
    out = None
    ###########################################################################
    # TODO: Implement the convolutional forward pass.                         #
    # Hint: you can use the function np.pad for padding.                      #
    ###########################################################################
    stride = conv_param['stride']
    pad = conv_param['pad']
    N, C, H, W = x.shape
    F, _, HH, WW = w.shape

    H_out = 1 + (H + 2 * pad - HH) // stride
    W_out = 1 + (W + 2 * pad - WW) // stride
    out = np.zeros((N, F, H_out, W_out))

    x_pad = np.pad(x, ((0,), (0,), (pad,), (pad,)),
                   'constant', constant_values=0)

    # 对原图片的每层进行卷积
    for pics in range(N):
        image = x_pad[pics]
        for filters in range(F):
            for H_move in range(H_out):
                for W_move in range(W_out):
                    image_conv = image[:, stride *
                                       H_move: stride * H_move + HH, stride * W_move: stride * W_move + WW]
                    filter_conv = w[filters, :]
                    out_pixel = np.sum(image_conv * filter_conv) + b[filters]
                    out[pics, filters, H_move, W_move] = out_pixel

    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = (x, w, b, conv_param)
    return out, cache

可视化中间的图像过程

这里输入了两个不同的输入图片
分别可视化了这个图片的不同weights

image_native

Convolution: Naive backward pass

愉快的简单计算back的过程，先不用考虑cost

input

dout
cache（x,w,b,conv_param) -> 参数是padding 和 stride

output

实现：conv是怎么求导的？

其实排除位置的改变之外，forward只进行了三个操作

把x padding为x_pad
wx_pad_conv + b -> 求出一个大小和filter相同的矩阵
把求出来的一个(HH,WW)的矩阵的所有值求sum
backward的思路
- 首先，每一张图片的每一个channel的，dout的大小和输出图片的大小一样
  - 应该是H_out = 1 + (H + 2 * pad - HH) // stride这样求出来的结果
  - 整个dout的size是(N,F,Hout,Wout)，其中N是之前图片的数量，F是新形成的图片的channel
  - 所以在for循环中，dout中选中[n,f,hout,wout]，就可以得到这个特点定的值，称为df
- df的得到方法是wx+b得到一个矩阵，然后再对这个矩阵求和
  - 因为求和实际就是累加，求导数的时候只要把每一个格子的dx，dw，db导数求出来，然后加在一起就行了
  - 因为公式就是wx + b，所以dx是w，dw是x，db是常数 -> 然后再把每个格子求出来的加在一起，注意各个矩阵的大小，dx应该是在x矩阵里取做卷积的部分，这部分的导数等于w乘df的和
- 最后，因为x被padding了，dx应该去dx_pad中没有被padding的部分，也就是从[pad:pad + H]

代码如下

def conv_backward_naive(dout, cache):
    """
    A naive implementation of the backward pass for a convolutional layer.

    Inputs:
    - dout: Upstream derivatives.
    - cache: A tuple of (x, w, b, conv_param) as in conv_forward_naive

    Returns a tuple of:
    - dx: Gradient with respect to x
    - dw: Gradient with respect to w
    - db: Gradient with respect to b
    """
    dx, dw, db = None, None, None
    ###########################################################################
    # TODO: Implement the convolutional backward pass.                        #
    ###########################################################################
    x, w, b, conv_param = cache
    N, C, H, W = x.shape
    F, _, HH, WW = w.shape
    _, _, H_dout, W_dout = dout.shape
    stride = conv_param['stride']
    pad = conv_param['pad']

    x_pad = np.pad(x, ((0,), (0,), (pad,), (pad,)),
                   'constant', constant_values=0)

    db = np.zeros_like(b)
    dw = np.zeros_like(w)
    dx_pad = np.zeros_like(x_pad)

    # print(dx_pad.shape)
    for pics in range(N):
        for filters in range(F):
            for H_move in range(H_dout):
                for W_move in range(W_dout):
                    # f=sum(wx_pad + b) (df is a number now)
                    df = dout[pics, filters, H_move, W_move]
                    # d for sum, size (HH,WW)
                    # dsum = df * np.ones((HH, WW))
                    db[filters] += df
                    dx_pad[pics, :, H_move * stride: H_move * stride + HH,
                           W_move * stride: W_move * stride + WW] += df * w[filters]
                    dw[filters] += x_pad[pics, :, stride * H_move: stride *
                                         H_move + HH, stride * W_move: stride * W_move + WW] * df

    dx = dx_pad[:, :, pad:pad + H, pad:pad + W]
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx, dw, db

Max-Pooling：Native forward

input

x, (N,C,H,W)
pool_param -> dict
- ‘pool_height’
- ‘pool_width’
- ‘stride’
不需要进行padding

output

out, (N,C,H’,W’)
- H’ = 1 + (H - pool_height) / stride
- W’ = 1 + (W - pool_width) / stride
cache(x,pool_param)

实现

直接找到相应的块然后求max
注意求max的时候要注意axis,我们需要求得是在一张图片每个channel上面的最大值，在这个式子里面因为已经确定了pics的值，实际上的out其实是一个三维的数组，所以应该求axis = (1,2)上面的最大值，而不是求(2,3上面的)

代码

def max_pool_forward_naive(x, pool_param):
    """
    A naive implementation of the forward pass for a max-pooling layer.

    Inputs:
    - x: Input data, of shape (N, C, H, W)
    - pool_param: dictionary with the following keys:
      - 'pool_height': The height of each pooling region
      - 'pool_width': The width of each pooling region
      - 'stride': The distance between adjacent pooling regions

    No padding is necessary here. Output size is given by

    Returns a tuple of:
    - out: Output data, of shape (N, C, H', W') where H' and W' are given by
      H' = 1 + (H - pool_height) / stride
      W' = 1 + (W - pool_width) / stride
    - cache: (x, pool_param)
    """
    out = None
    ###########################################################################
    # TODO: Implement the max-pooling forward pass                            #
    ###########################################################################
    N, C, H, W = x.shape
    pool_height, pool_width, stride = pool_param['pool_height'], pool_param['pool_width'], pool_param['stride']

    H_out = 1 + (H - pool_height) // stride
    W_out = 1 + (W - pool_width) // stride

    out = np.zeros((N,C,H_out,W_out))
    for pics in range(N):
        for h_out in range(H_out):
            for w_out in range(W_out):
                out[pics,:,h_out,w_out] = np.max(x[pics,:,stride * h_out: stride* h_out + pool_height,stride* w_out: stride*w_out + pool_width],axis = (1,2))

    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = (x, pool_param)
    return out, cache

Max-pooling: Native backward

input

dout, size = (N,C,W_out,W_out)
cache

output

dx, size = (N,C,W,H)

实现

max的值在实际上是一个router，local gradient对于最大的值的地方是1，其他值的地方影响是0
需要找到x里面值等于最大值的坐标，然后把这个坐标的dx改成对应dout的值（因为链式法则应该dout * 1），其他地方的dx都是0
关于找到这个点的坐标
- 我用了显得很傻的方法，在x的范围里面找到这个范围里最大的坐标，用了很多圈循环
- 实际上可以从max的值找到原来的坐标
  - numpy.unravel_index(indices, dims)
  - 结合np.argmax，返回最大值的坐标 -> ind = np.unravel_index(np.argmax(a, axis=None), a.shape)
  - 这样的话找到的是在每个max的框框里最大值的坐标，在这个框框的范围里找到这个坐标就是需要改变的地方

def max_pool_backward_naive(dout, cache):
    """
    A naive implementation of the backward pass for a max-pooling layer.

    Inputs:
    - dout: Upstream derivatives
    - cache: A tuple of (x, pool_param) as in the forward pass.

    Returns:
    - dx: Gradient with respect to x
    """
    dx = None
    ###########################################################################
    # TODO: Implement the max-pooling backward pass                           #
    ###########################################################################
    x, pool_param = cache
    N, C, H, W = x.shape
    pool_height, pool_width, stride = pool_param['pool_height'], pool_param['pool_width'], pool_param['stride']

    _,_,H_out,W_out = dout.shape
    dx = np.zeros_like(x)

    for pics in range(N):
        for channels in range(C):
            for h_out in range(H_out):
                for w_out in range(W_out):
                    # for H in range(stride * h_out, stride* h_out + pool_height):
                    #     for W in range(stride * w_out, stride * w_out + pool_width):
                    #         if x[pics,channels,H,W] == np.max(x[pics,channels,stride * h_out: stride* h_out + pool_height,stride* w_out: stride*w_out + pool_width]):
                    #             dx[pics,channels,H,W] = dout[pics,channels,h_out,w_out]

                    ind = np.unravel_index(np.argmax(x[pics,channels,stride * h_out: stride* h_out + pool_height,stride* w_out: stride*w_out + pool_width]), (pool_height,pool_width))
                    dx[pics,channels,stride * h_out: stride* h_out + pool_height,stride* w_out: stride*w_out + pool_width][ind] = dout[pics,channels,h_out,w_out]
                    # print(ind)
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx

Fast layers

在cs231n/fast_layers.py里面直接提供了比较快版本的计算方法

The fast convolution implementation depends on a Cython extension; to compile it you need to run the following from the cs231n directory:

1	python setup.py build_ext --inplace

记得重启一下jupter

Testing conv_forward_fast:
Naive: 5.283360s
Fast: 0.014807s
Speedup: 356.809600x
Difference:  4.926407851494105e-11

Testing conv_backward_fast:
Naive: 9.893734s
Fast: 0.015421s
Speedup: 641.578958x
dx difference:  1.949764775345631e-11
dw difference:  5.155328198575201e-13
db difference:  3.481354613192702e-14

Testing pool_forward_fast:
Naive: 0.212025s
fast: 0.002980s
speedup: 71.143680x
difference:  0.0

Testing pool_backward_fast:
Naive: 0.391351s
fast: 0.012568s
speedup: 31.138711x
dx difference:  0.0

可以发现fast版本conv的速度会快300倍，而pooling也会快几十倍

conv sandwich layer -> 已经写好了，conv + relu + pool

Three-layer ConvNet

cs231n/classifiers/cnn.py,implement一个三层的CNN结构

conv - relu - 2x2 maxpool - affine1 - relu - affine2 - softmax
输入图片的minibatch为(N,C,H,W)

init

input_dim: (C,H,W)是每张图片长什么样子
num_filters: conv层里面filter的个数
filters_size，直接把高和宽统一成一个数字了，反正都是方形的
hidden_dim：用fc层的数量
num_classes: 最后输出的class的数量
weight_scale：初始化的时候的scale
reg：L2
dtype：计算所用的datatype（如 np.float32)

loss + gradient

需要初始化三层的参数，W123和b123
初始化weights（正态分布）和bias（全是0） -> 注意fc和conv层的不一样
因为在loss中有帮助input的大小保持的操作，所以第二层的图片可以不考虑padding和stride的变化
W1的大小是filter的大小(F,C,HH,WW)，需要filter的数量，channel的数量，以及每个filter的大小，b1是(filter,)
conv_relu之后进行了一次max pool，所以图片的大小缩小了一半
后面两个affine的大小就跟输入，hidden_num和最后的num_classes有关系了，b的大小跟输出走
- 注意第二个affine之后不需要relu
loss用之前写好的softmax
注意需要regularization
直接用之前写好的把gradient back回去就可以了

Sanity check loss¶

在建立一个新的net的时候，第一件事就应该是这个

用softmax的时候，我们希望random weight，没有reg的结果是log(C)
如果加上了reg，这个数量会轻微增加一点

overfit small data

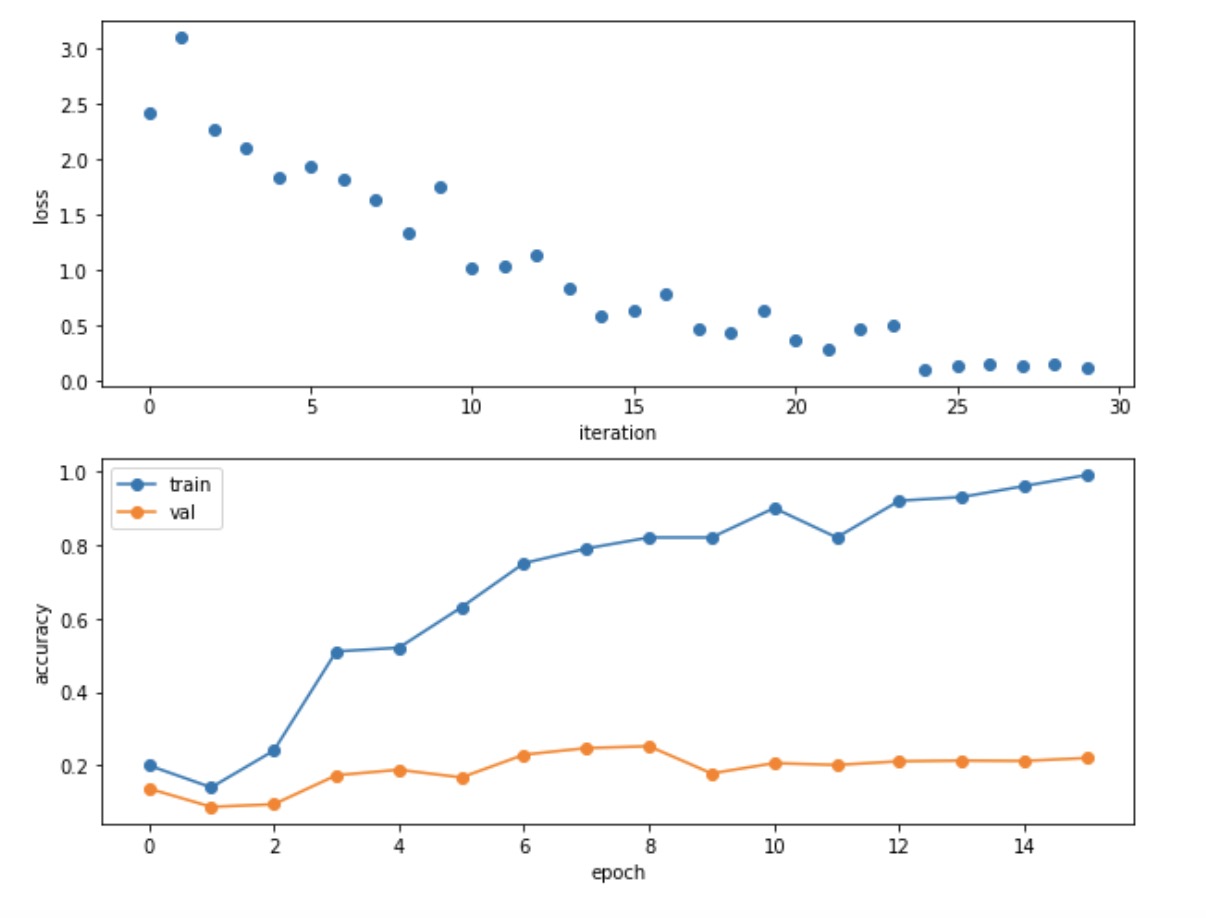
直接用非常少的数据来训练一个新的网络，应该能在这个上面overfit
应该会产生一个非常高的训练精度和非常低的val精度
注意在loss里面的时候需要记录下来scores，我就是因为变量名写错了所以一直bug
最后训练出来的train_acc接近100%，而val_acc只有百分之20

acc

np.random.seed(231)

num_train = 100
small_data = {
  'X_train': data['X_train'][:num_train],
  'y_train': data['y_train'][:num_train],
  'X_val': data['X_val'],
  'y_val': data['y_val'],
}

model = ThreeLayerConvNet(weight_scale=1e-2)

solver = Solver(model, small_data,
                num_epochs=15, batch_size=50,
                update_rule='adam',
                optim_config={
                  'learning_rate': 1e-3,
                },
                verbose=True, print_every=1)
solver.train()

训练这个三层的网络

直接用所有数据训练这个网络，应该得到的train_acc应该在40%

最后训练了1个epoch，980次iter

1	(Epoch 1 / 1) train acc: 0.496000; val_acc: 0.489000

可视化第一层的filter

vis

Spatial Batch Normalization

在之前我们已经看到BN对于训练NN很有用了，根据15年的一个论文，CNN里面也可以用BN -> SBN
普通的BN会接收(N,D)大小的input，并且output是同样的大小，normal的时候用data的总数N
CNN里面，input为(N,C,H,W)，output大小相同（也就是和X同样尺寸）
如果用卷积得到的特征map，we expect the statistics of each feature channel to be relatively consistent both between different imagesand different locations within the same image -> 所以在SBN里面，计算对每个C里面的特征计算mean和var

Spatial batch normalization: forward

cs231n/layers.py
input:

x,(N,C,H,W)
gamma,scale parameter (C,)
beta,shift param (C,)
bn_param: dict
- mode: train/test
- eps
- momentum
- running_mean
- running_var
  output
out,(N,C,H,W)
cache, back的时候需要的东西

注意，可以调用之前写的关于 batchnorm_forward 的内容，代码应该少于五行

这里需要用到多维数组的转置，需要把矩阵变成（N H W） * C的格式，然后在求完bn之后再转回去
- 之前fc里面使用的时候的大小是(N,D)，这样的话是在所有的N上面取平均
- 这里的C代替了以前的D，NHW代替了以前的N(把每张特征图看做一个特征处理（一个神经元），这里的特征图指的是一层的东西)
- 这里用到的是一张特征图里面的所有神经元的参数共享

Spatial batch normalization: backward

输入dout(N,C,H,W)和cache，输出dx，dgamma和dbeta
同样也是直接调用之前的，变形方法和之前一样

Group Normalization

同样原理，把维度变化之后使用
np.newaxis()