学习OpenCV十八章_Camera models & calibration

Posted on | Edited on | In , ,

camera models & calibration

物体会吸收一部分的光，然后反射一部分的光，反射的光就是他自己的颜色，这个光被我们的眼睛（或者相机）接收，然后投影到我们的视网膜（或者相机的图片）上，这之间的几何关系在CV上面非常重要

其中一个非常简单的模型就是pinhole camera model。光穿过一面墙上的一个小的aperture，这个是这章的模型的开始，但是真实pinhole模型不是很好因为他不能快速曝光（聚集的光不够）-> 眼睛会更厉害一点，但是len还会distort图片。

这章的目的：

  • 如何camera calibration
  • 纠正普通的pinhole模型的len的偏差
  • calibration也同样是获取三维世界的主要方式，因为一个场景不仅仅是三维，他们还有物理的空间和体积，所以获取pixel和三维诗句坐标的关系也很重要
  • 18章纠正的是len的distortion，19章构建整个3D的结构

homography transform -> 一个非常重要的要素

camera model

  • 投影到image plane上面，结果在这个plane上面总是对焦的focus，图片的大小和这个焦距的长度有关
  • 对于理想的pinhole来说，image plane到pinhole的距离就是准确的焦距

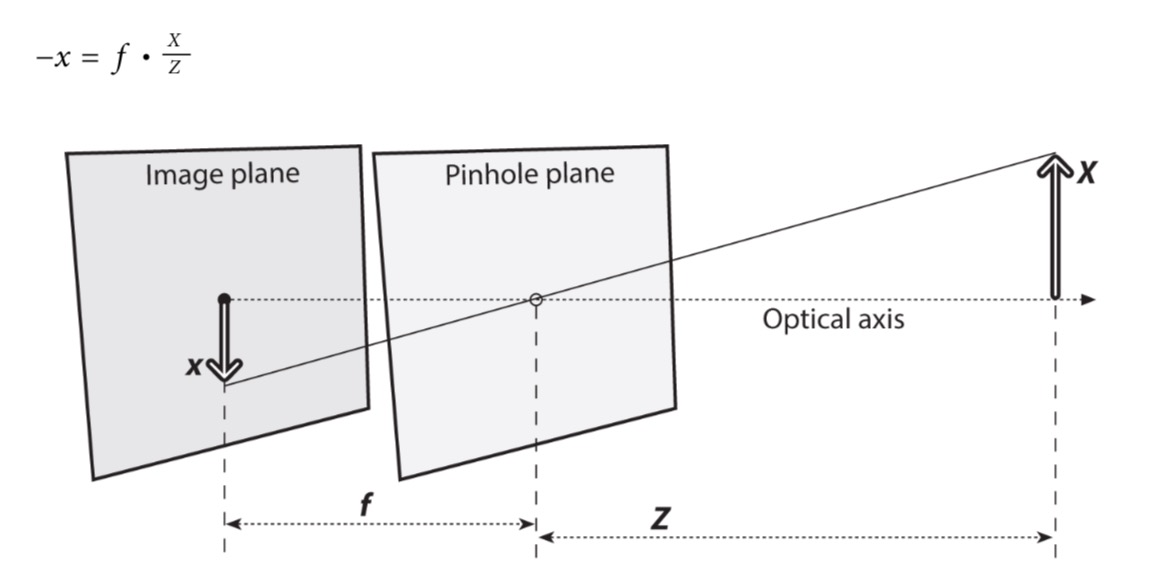
pinhole

  • 从这个基础的模型上 -> 得到一个计算起来更加简单的模型
    • 交换pinhole和projection plane的位置
    • 现在pinhole的位置变成了projective plane的中心
    • 每一个离开物体表面（Q）的光线都朝着projection center走
    • 在横轴和投影面上的交点被定义为principal point
    • 这个新的平面和以前的projective平面一样，上面投影上的物体也都是和原来一样的尺寸
    • 换了模型之后没有了负号：x/f = X/Z

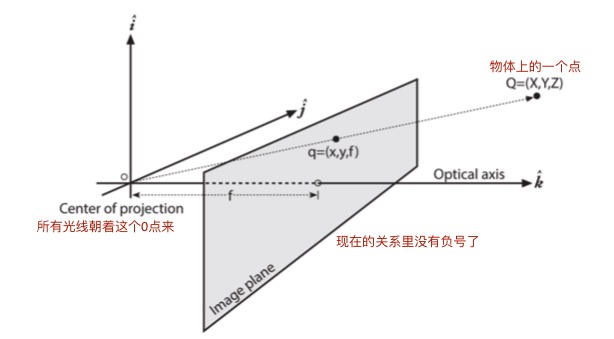
pinhole2

  • 在理想的模型里可能觉得这个principal point就是image的中心，但是实际上中心不会在横轴和投影面的交点上
    • 引入了两个新的参数 cx 和 cy
    • 这两个参数实际上就是中心点的偏差（平面上的偏差），所以得到投影在image plane上面的实际坐标如下

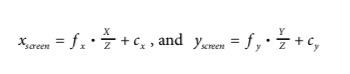
pinhole3

  • 在上面的公式里面用了两个不同的f，fx和fy，这是因为
    • 在实际的图片里来说，其实每个像素格不是正方形而是长方形的
      • fx = 实际的focal length * sx（每个mm里面的像素数量） -> 最终得到的fx是像素格
    • 注意：
      • sx和sy在calibration的时候并不能直接测量
      • physical focal length也不能被实际测量
      • 我们只能得到这两个东西的乘积，f

basic of projective geometry

  • projective transform -> 把physical world里面的一组点Qi（Xi,Yi,Zi）map到一张图片上面(xi,yi)的过程
    • 用这个东西的时候，一个比较方便的方法是用homogeneous coordinates
      • associ‐ ated with a point in a projective space of dimension n are typically expressed as an (n + 1)-dimensional vector (e.g., x, y, z becomes x, y, z, w), with the additional restric‐ tion that any two points whose values are proportional are, in fact, equivalent points
    • 投影平面上面的维度是两维，我们可以把它表示成三维的东西 -> 把现在存在维度的数字除以增加的维度的值就可以得到以前的值
    • 用这种办法，可以把之前的fx，fy,cx,cy重新组织成一个矩阵：camera intrinsics matrix
    • 下面这个形式重新乘回来就是之前的关系

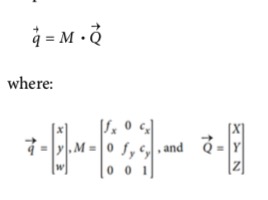
matrix

  • 在opencv里面也有得到homogeneous coordinates和由结果反推回来的函数

  • 注意，在pinhole里面的成像速度是非常慢的，如果需要更快速地形成图片，我们需要通过lens来聚焦非常广范围里面的光 -> 但是结果就是lens会产生distortion

Rodrigues Transform

  • 在三维的范围里，经常会使用一个3x3的矩阵来表示一个物体的旋转
    • 只要把需要旋转的vector乘上这个mat就可以得到相应的结果
    • 但是不是很好直观的得到这个旋转矩阵
  • 介绍一种在opencv里面的表示方法 -> 更容易直观的理解意思
    • 本质上来说就是用一个vector表示每个角度上需要旋转多少
    • Rodrigues Transform指的就是矩阵表示法和向量表示法之间的关系
  • 数学原理：余弦定理？（知道两个向量可以求出来他们之间的角度）
  • 这两个关系之间可以很轻易的互相转化，opencv里面也有相应的库

lens distortion

  • 在实际使用中因为制造球形的镜头更容易一些，并且很难测量是不是平的，所以lens都会产生distortion
  • 在这部分介绍了两种主要得distortion，how to model
    • radial distortion -> 镜片的形状产生的
    • tangential distortion -> 组装整个相机的时候产生的

radial

  • 相机的distortion一般都会产生在接近imager边缘的部分（fisheye effect）
    • 远离lens中心的部分比起中心部分会折叠更多，所以如果投影一个正方形，边的部分都会鼓起来
    • 如果相机比较便宜的话（web camera），周围的折叠会更多，而好的相机会更注重减少radial distortion的效果
  • 对于辐射的畸变来说，distortion会随着接近边边而增加
  • 在实际中这个畸变很小，所以可以用泰勒级数的r=0附近展开来解决
    • 对于比较便宜的web camera，可以选用k1或者k2
    • 对于鱼眼这种畸变很大的，可以用k3
  • 在distort之后的位置可以用以下的公式表示
    • (x,y)是原来的位置，corrected是教政治和的位置
    • r是离开中心的半径

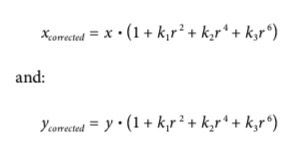
radial

tangential

  • 在制造相机的时候，lens和image plane没有完全平行导致的，所以投影上去会是一个几何变换
  • 这个distortion基本是由两个参数组成：p1和p2

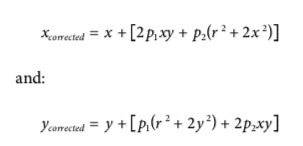
tangential

  • 总结下来，在相机的distortion里一共有五个参数，k1k2k3p1p2，这五个函数构成了一个distortion vector(5x1)
  • 虽然在图像里面还有一些其他的畸变，但是因为影响没有这两个大所以opencv没有考虑这部分

calibration

  • 上一部分得到了如何表示相机的参数以及distortion的参数
  • 这部分考虑如何计算这些参数
  • 其中一个函数clibrationCamera()
    • 用相机去照一个已经知道结构的东西，里面有很多已经定义好了的点
    • 通过这个可以得到相机的相对位置和角度，同时也可以得到intrinsic parameters

平移矩阵和旋转矩阵

  • 对于每张照的图片的物体，这个物体的pose可以用一个旋转矩阵+一个平移矩阵描述，也就是用这个矩阵把现实世界中的点转化到投影平面上

旋转矩阵

  • 旋转运动无论在多少维都可以被描述为：一个坐标的vector乘对应大小的方阵 -> 用一个新的坐标系来描述这个点的位置 -> 其实也就是改成了极坐标系？
  • 三维范围里面的旋转可以用两个角度表示
  • 绕着x，y，z三个方向旋转的角度以及对应的矩阵是这个样子的

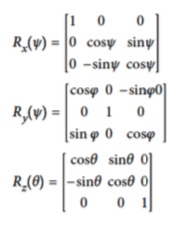
rotation

这三个方向的R乘在一起就是最后的旋转矩阵R，但是这个的方向是反着的，所以还需要一个transpose转回来

平移矩阵

  • 平移矩阵用来描述怎么从一个坐标系统shift到另一个坐标系统 -> 也就是一个从第一个坐标系原点到第二个坐标系原点的offset
  • 在calibration的时候，就是从物体坐标系的原点到了相机坐标系的原点
  • 平移矩阵： T→ = origin_object − origin_camera.

综合

  • 结合上面两个矩阵来说，从object上面的一个点投影到camera plane上面的一个点的关系为
    • Pc→ =R⋅(Po→ −T→) 注意分清楚这里面的矩阵和向量
  • 把上面的这个公式，再加上camera自己的intrinsic-correction。整体就是opencv里面需要求的所有部分
  • 所求参数
    • 三维的旋转用三个角度表示，三维的平移用三个parameter表示(x,y,z) -> 现在得到了6个参数
    • 相机的intrinsic mat(fx,fy,cx,cy) -> 一共四个参数
    • 现在一共需要求10个参数（但是相机的intrinsic是不变的）
  • 求参数 ->
    • 在求解的时候，如果使用一个平面物体，那么每张图片都可以得到8个参数（位置的6个会随着图片变化 + 只能用两个参数来求intrinsic）
    • 至少需要2张图片来得到所有的参数

calibration boards

  • 从原则上来说，任何有特征的东西都可以被用来calibration，包括棋盘，圆格，randpattern，arUco等等,有些方法是基于三维的物体的基础上的，但是二维平面的物体更好操作
  • 在这里主要选择的是用棋盘进行calibration

关于chessboard的函数

cv::findChessboardCorners()

  • 可以用这个函数找到棋盘的corners，
  • param
    • 需要输入8bit图片
    • 需要输入这个棋盘每行每列应该有的格子数（计算的是内部点）
    • 输出的是这么corner的坐标
    • 可选flag决定需不需要多余的filter

cv::cornerSubPix()

  • 上面一步找到的只是corner的大概位置
  • 在find corner里面自动call了这个函数，为了能得到更精确的结果
  • 如果需要得到更精确的结果，可以重复的call这个函数，但是会有tighter termination criteria

cv::drawChessboardCorners()

  • 为debug用，更明确的画出来找到的corner
  • 如果没有找到所有的，会把其他可能的用红色circle画出来，如果找到了，每一行的颜色会不一样

下一步转到perspective transform，这个transform会形成一个3x3的homography mat

关于circle grid的函数

cv::findCirclesGrid()

  • 和上面的棋盘没有什么本质的区别，主要就是画出来一个是黑白格，另一个是白色的背景上面有黑色的圆点，输出小圆点的位置
  • 这个方法需要圆点是对称的，上下一组算做一行，竖着一列算一列，怎么数非常重要

Homography

  • planar homography是一个平面到另一个平面的projection mapping，所以从一个2D平面到相机平面的过程就是一个planar homography
  • 用矩阵的乘法就可以表示这个过程

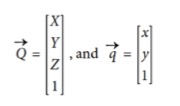
projection mapping

其中Q是现实中的点，q是成像器上面的点，整体关系为：q→ = s ⋅ H ⋅ Q→

  • s，一个随意的scale参数，homography就是由着一个参数决定的
  • conventionally factored H, H由两个部分组成
    • physical上面的transformation，实际就是我们看到的这个物体的位置W = [R,t→]
    • projection，取决于相机的intrinsic
  • q→ = s ⋅ M ⋅ W ⋅ Q→，其中M是相机的intrinsic mat

  • 我们希望Q不是给所有空间定义的点，而是一个定义在我们看的平面上面的坐标，这样计算起来会方便（三维转二维）

    • 所以把Q里面的Z的坐标改成了0，这样旋转矩阵就会被简化为一个3x1的列
    • 并且第三个列乘了Z的0之后就被消掉了
    • 最后就可以把H表示出来了 -> 3x3 = intrinsic(3x3) x (rota + trans)(1x3)
      H

  • 在计算homography mat的时候，用了多张同样内容的东西来计算translation和intrinsic

  • 三个旋转，三个平移 -> 每张图片有6个未知的参数
  • 每张图片可以得到8个等式
    • 把一个正方形mapping成一个四边形可以得到4个不同的(x,y) points
    • 所以每多一张图片就可以多出来计算两个新的参数的机会
  • 这样看，pdst→ = H * psrc→，反着也可以推回来，这样我们就算不知道M也可以计算H，或者说我们是用H来计算M
  • 在opencv里面，cv::findHomography()可以用take一堆有关系的点然后返回他们之间的homo mat，点越多计算的越准确
  • 虽然有其他的方法可以计算结果，但是对测量误差不是很友好

three robust fitting methods

  • method to cv::RANSAC
    • 随机的选择提供的点的subset，然后只用这些subset来计算homo mat
    • 然后把剩下的数据拿来计算一下靠谱和不靠谱的
    • 最后保存最有潜力的inliers
    • 在现实中比较好用，可以过滤掉一部分噪音
  • LMeDS algorithm
    • 减少median error
    • 不需要更多的info和data来运行
    • 但是it will perform well only if the inliers constitute at least a majority of the data points
  • RHO algorithm
    • 加权的第一种方法，运行速度更快

camera calibration

棋盘corner个数

  • 到底有多少参数
    • camera intrinsic 四个
    • distortion五个（或者更多）三个辐射（可以增加到6个） + 两个平移
      • 这五个参数是从2D -> 2D的
      • 三个corner points可以得到6个信息，足够处理这五个参数
      • 所以一张图就够了（只是原则上这么说）
    • extrinsic parameters，这个东西的实际位置
  • 但是因为intrinsic和extrinsic之间有对应的关系，一张图片并不够 -> 因为在一张图片里还需要计算extrinsic的部分
  • 假设有N个corner，一共有K个images（不同的position）
    • 一共会有 2 N K个，2是x,y的坐标会有两个，然后N个corner，K个图片
    • 暂时忽略distortion的参数，这样需要4个in和6K个ex（因为每张图片的ex都是不一样的）
    • 2NK >= 6K + 4
      • 如果N = 5，只需要一张图片就可以解决。但是为了得到homo mat，至少需要两个K(之前说到过的)
        • 无论检测到多少corner，得到的有用信息就是四个角 -> 由此推测至少两个K
    • 在实际的应用里面，一般需要7x8，至少十张图，这样受到noise的影响更小

具体的数学计算

  • 为了简单，首先假设在calibration的时候根本没有distortion
  • 对于每个view，会得到一个Homo mat，把这个mat拆成一个列向量(3x1)
    • 在前面也知道H可以拆成M和一个[r1,r2,t]的向量相乘，再乘上一个scale s
    • H=[h1,h2,h3] =s⋅M⋅[r1,r2,t],其中landa是1/s: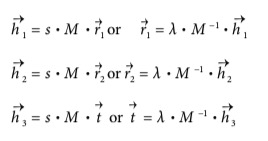
      H
  • 旋转向量的基底(orthogonal)是互相垂直的，因为已经把scale这个参数提出去了，所以可以直接认为r1和r2是基了，这样的话他们的点乘是0
    • 把r1和r2用M和h来表示，这样的话r1r2等于0就可以转化成一个hM的公式
    • r1和r2的模也相等，所以可以继续得到一个等式
  • 设置一个矩阵B等于M.-T * M-1，这样可以计算出来B的值(B算出来是对称的)
    • 把B带回原来的等式，化简，然后把K个等式叠加在一起
    • 这样就可以推出来几个参数的表达式

calibration的函数

cv::calibrateCamera().来解决calibration的问题

  • 得到的结果包括in mat, dis_co, 旋转向量和平移向量
    • 输出的in mat的大小是3x3
    • 输出的dis_co的大小取决于用多少级的distortion，一般来说是4，5个的已经对fisheye足够了，8个的话calibration的精度就特别高了
      • 如果需要高精度的calibration的话，需要的图片数量也会疯狂增加
  • 输入的部分包括
    • 物体的坐标，指的是在chessboard上面的坐标点，是二维的点，其实也就是第几个格子？
      • 注意这里，统计的单位是格子，所以如果想要得到physical上的距离，需要在calibration board上量出来一个格子的长度，然后乘这个格子的数量
    • image上面的坐标，corners
  • 一口气计算所有的参数不是很好实现，一般使用的方法是先固定一部分计算另一部分，然后再固定另一部分计算这一部分。当所有的东西都估计的差不多了，再一起计算
  • 最后还有一个参数是termination criteria，终止的基准 -> epsilon 会根据一个error来计算是否终止

只计算extrinsic

cv::slovePnP()

  • 有的时候我们已经得到了相机的intrinsic，只希望得到object的位置
  • 大部分内容和上面都是一样的，除了
    • 物体的位置只需要一个view
    • distCo和intrinsic都是自己设置好的，不需要计算

cv::solvePnPRansac()

  • 上面的函数对于outliers的robust效果不是很好，对于chessboard来说，这个robust不是很重要，因为棋盘自己本身已经很可靠了。但是对于现实世界中的物体来说不是这么可靠
  • 加入了RANSAC部分？

Undistortion

  • 在calibration里面有两个需要解决的事情，一个是distortion，一个是三维表达的正确性
  • opencv自己有一个可以用的方法
    • cv::undistor() -> 可以一瞬间完成
    • cv::initUndistortRectifyMap() + cv::remap() -> 在video上面使用的时候效率更高一些

undistortion map

  • 在把一张图片undistort的时候，我们需要把每个像素都对应到output里面对应的地方去，有几种不同的表达方法
    • 2-channel float
      • 有一个对于NxM的remapping，表示成NxM的array，有两个channel（分别对应X和Y方向的remap），里面是浮点数
      • 对于每一个输入的像素位置(i,j)，有一个对于这两个位置的向量，来表达这两个量应该哪里去
      • 如果计算出来的结果不是一个整数，那么用interpolation来计算最后应该占的格子的数量
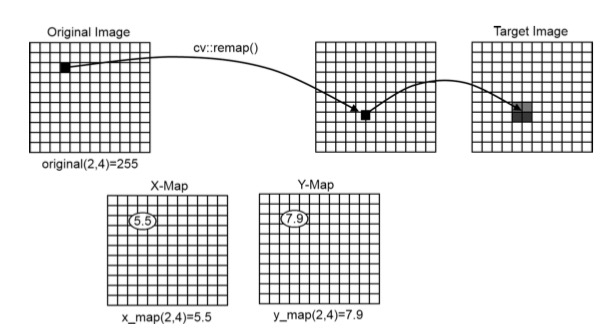
        remap
    • 第二种表达式是 2-array float，每一个array是一个channel的移动
    • 第三种是fixed point，计算的速度更快一点，但是需要提供的信息的精确度更高

cv::convertMaps()

  • 因为有上面的三种不同的表达形式，所以这个函数用来在各个形式之间转变

cv::initUndistortRectifyMap()

  • 从刚才的部分知道了到底什么是undistortion map，现在开始讨论如何计算这个map
  • 现在先从单目相机开始monocular，如果双目的话可以直接计算depth（下一章）
  • 步骤，分开是因为计算map只需要一次
    • 先计算undistortion map
      • cv::initUndistortRectifyMap()
      • 输入的参数是intrinsic mat和distortion coefficient（从camera calibration得到的）
      • 可以得到一个新的camera mat，这样的话即使不undistortion也可以得到正确的图片（在多个相机的calibration的时候比较重要）
      • 最后会输出两张map
    • 然后在图片上undistort

cv::remap()

  • 当计算了上面的map之后，就可以用remap这个函数进行校正了
  • 输入的map的种类也是上面提到的三种都可以

cv::undistort()

  • 如果只有一张图片，或者对于每张图片都需要重新计算map的时候，就需要用这个函数了（所以在项目里面用这个的速度会变慢）

sparse undistortion cv::distortionPoints()

  • 如果我没有整张图片，只有一些图片上的点，然后我只关心这些图片上的点，可以用这个函数计算这张图片上面关注点的位置