学习OpenCV第19章，投影和3D视觉

Chapter 19

首先会讨论从3D得到2D信息，然后再讨论从2D推断3D信息
如果没有多张图片是很难得到靠谱的3D信息的：

• 通过stereo vision
• 通过motion

Projections

• 得到了物体在三维里面的位置之后，因为我们在18章已经calibration了相机，所以可以得到这个点在图片里面的位置
• 提供了一个函数projectPoints来投影一系列的点，针对刚体
  • a list of loca‐ tions in the object’s own body-centered coordinate system
  • 加上了平移和旋转，相机intrinsic和distortion
  • 最后输出在画面上的店

Affine and Perspective Transformations

affine是针对一个list或者一整张图片进行的，可以把一个point从图片的一个location移动到另一个location，perspective trans更多的是针对一个矩形图片 -> related to prspective transformation

总结不同的函数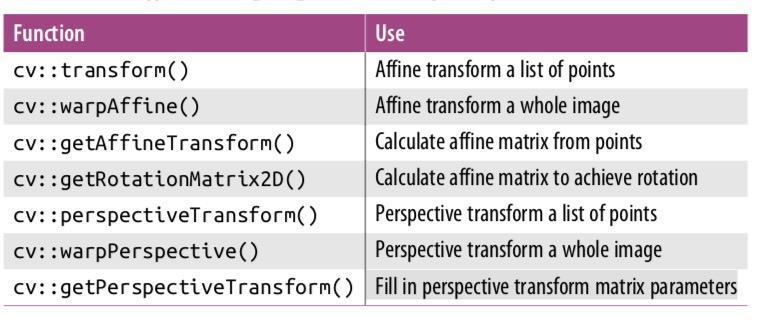

Bird’s-eye-view trans（p699）

• 在robtic巡航的时间，经常把排到的画面变成从上往下看的bird-view
  • 需要相机的intrinsic和distortion （把棋盘放在地上进行calibration）
• 步骤
  • 首先读取相机的参数和distortion model
  • 找到地面上已知的店（比如chessboard），找到至少四个点
  • cv::getPerspectiveTransform()计算地面上已知点的homography H
  • cv::warpPerspective()形成bird-eye-view

three-dim pose estimation

物体的三维pose可以从

• 一个相机：必须先考虑情况惹
• 多个相机捕捉：从多个不同图片来推断，这样即使是不知道的东西都可以操作

single camera

• 如果我们知道一个object，我们需要知道这个东西在他自己坐标系里面关键点的坐标
• 如果现在给了一个新的view point，可以根据关键点的位置来推断

cv::solvePnP()

• 用来计算一个know object的位置
• 从图片里面提取特征点，然后计算不同点的位置，这个问题的解是应该是唯一的
• PNP问题不是每次都有唯一的解
  • 如果没有足够的关键点，为了保险起见应该有足够的店
  • 或者当物体离得特别远（这时候光线接近于平行了，就不好判断了）

总的来说，单目视觉和人自己的眼睛（单只）看东西的感觉差不多，不能获得精确的大小，还会产生一些错觉（比如把大楼的窗户设计的小来显得楼更高）

Stereo Imaging

在电脑中，通过计算在两张图里面都出现的点的位置来计算，这样就可以计算这个点的三维位置。虽然这样计算的计算量很大，但是可以通过一些方法来压缩搜寻的范围，从而得到相应的结果。
主要分为4步：

• 在数学上remove掉相机lens的辐射和平移distortion -> undistortion
• 调整相机之间的角度和距离 -> rectification。这一步输出之后的两张图片应该是row-aligned的（frontal parallel）
• 找到左右两张图相同的feature -> correspondence。这一步的输出是一个disparity map，输出的是两个图中相同特征点的x坐标方向上面的disparity
• 最后可以把disparity转换成triangulation，这一步叫做reprojection，这样输出的就是depth map了

triangulation（找到disparity和depth的关系）

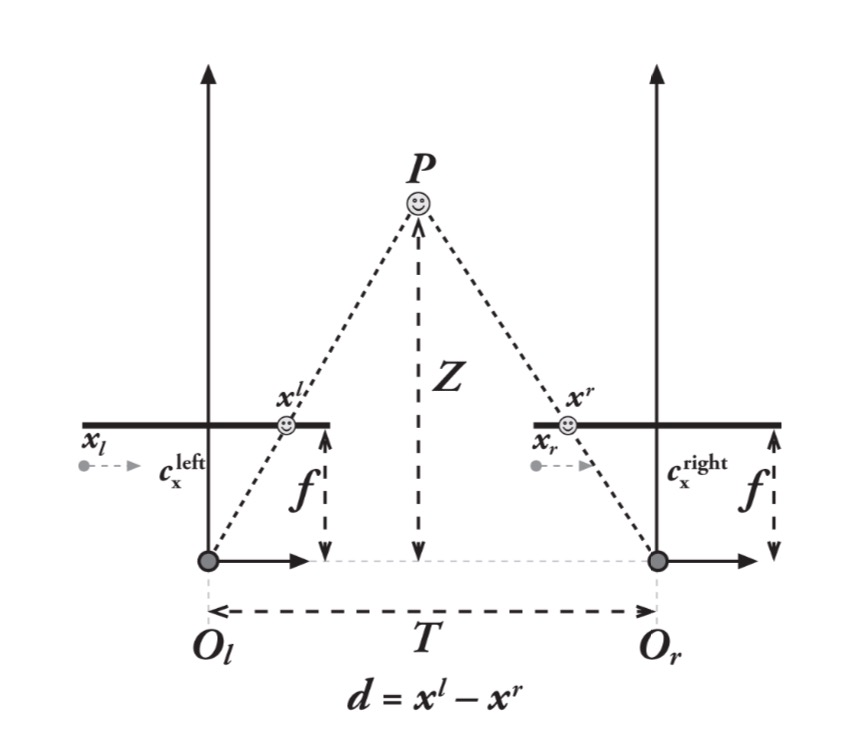
• 整体概念如上图所示，在这张图里我们假设系统已经完全undistort，aligned（两张图片的行和行对上了）了，两个相机的平面完全相同，焦距也相同，并且两个相机的cx已经被calibrated好了（相同）
• 这时，这个物体点P的depth和disparity是成正比的，求出来的disparity是：xl - xr（xl和xr都是根据各自的相机中心的坐标）:

T - (xl - xr)/Z - f = T/Z

• 这个关系虽然是正比但是不是线性的
  • 当disparity接近0的时候，小的disparity的差异会引发非常大的depth的差异
  • 当disparity非常大的时候，disparity的改变不会对depth引起太多的影响
• 最终，stereo的系统只在比较接近相机的部分有比较高的depth resolution（如下图所示）

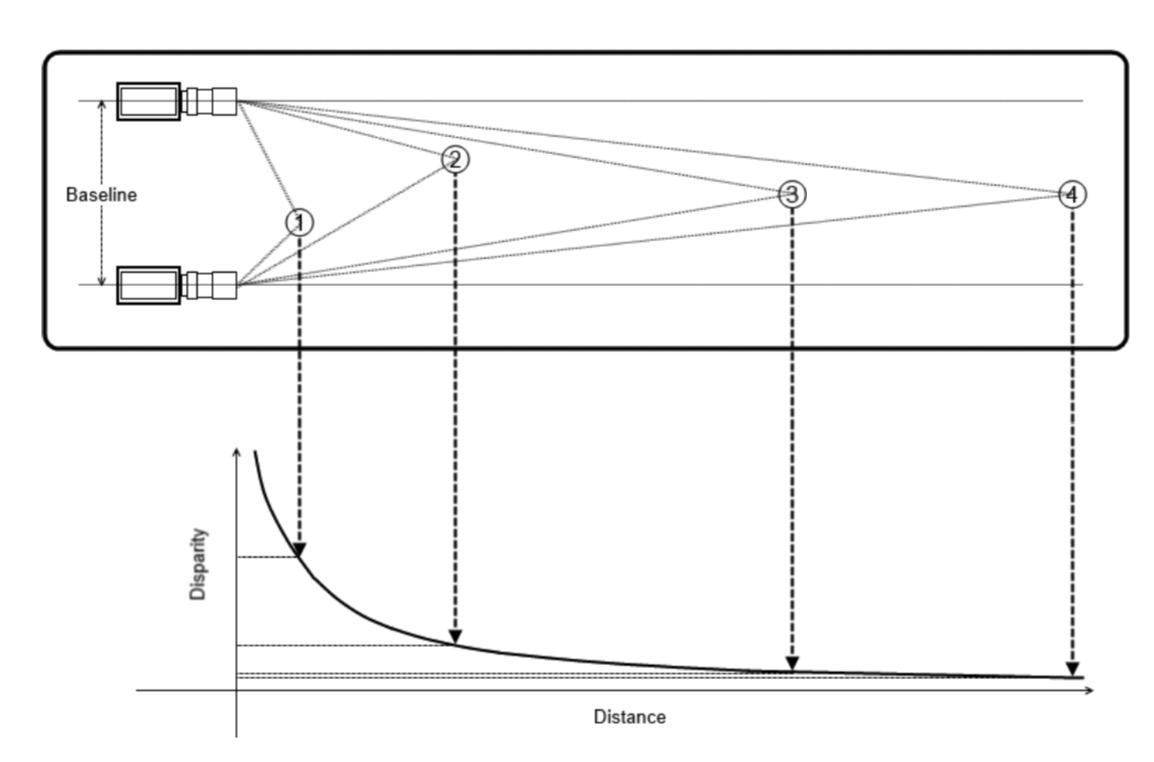
• 上面的例子是二维转一维的，实际在OpenCV的系统里面是三维转二维的
• 在实际的应用里面相机不是那么理想的共线的，要尽量确保共线，才不会引起太多的distortion。最终的目的是通过math的计算让他共线，而不是在物理上共线
• 除此之外，还需要保证相机的拍摄是同步的，避免在拍摄的时候会有东西移动

Epipolar Geometry（简化双目模型）

stereo image system的模型：

• 组合了两个pinhole model
• 加入了新的points epipoles

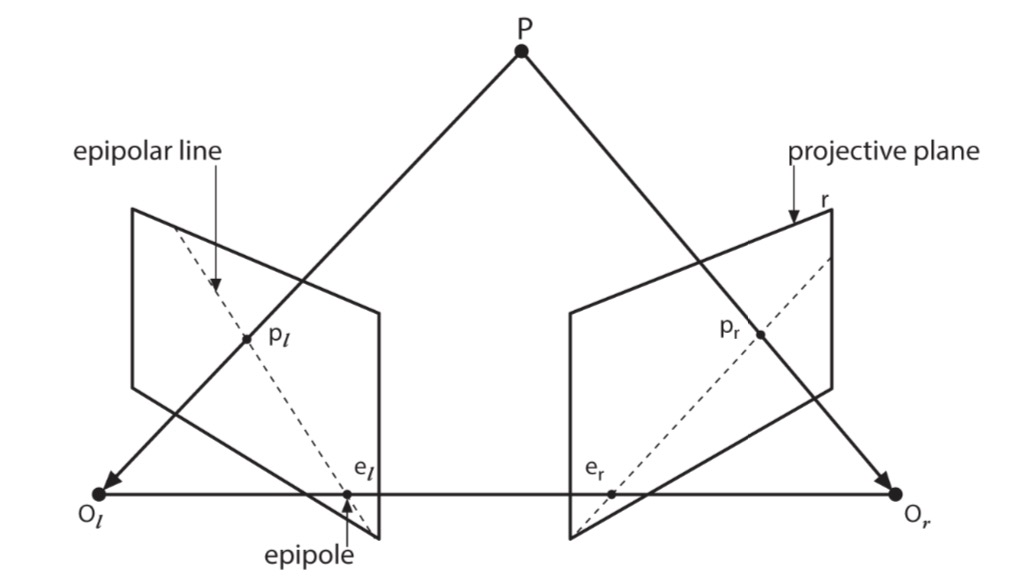
主要点：

• 对于每个相机都会有一个投影的中心O，并且有两个和这个相关的投影平面
• 在现实中的物体P会在两个投影平面上分别有投影pl和pr
• el或者er，定义是另一个相机的中心在这个投影平面上的投影，el和pl可以形成一条epipolar line

得到要义

• 每个三维的点，都会在每个相机上面得到一个epipolar的，这个点和pr/pl的交点就是epipolar line
• 一个图片里面的feature，在另一个图片里面必须在相对应的epipolar line上面（epipolar constraint）
• 上面那个定义意味着：可以把在图片上寻找特征从二维（图片）降低到一维（线）
• 并且图片的order会保存，比如一条线在两张图里面都是水平的

The Essential and Fundamental Matrices

• E Mat：包括了两个相机的translation和rotation
• F Mat：包括了E的信息，以及相机的intrinsic（在pixel的层面上关联两个相机）
• 二者的区别
  • E只知道两个相机的关系，不知道任何关于图片的信息，只在物体的层面上关联了两个相机
  • F关联了两个照片在各自图片坐标系里面的关系

E math + F mat（p713，还没有怎么看）

• 在左边的相机里，观察到的点是pl，在右边的相机观察到的点是pr
• pr = R（pl - T）

cv::findFundamentalMat

Computing Epipolar Lines(计算上面模型里面的那条线)

• 有了F Mat之后希望可以计算上面的epipolar line。每一个图片里面的line都会在另一张图片里有一个对应的line
• line用一个三个点的vector来表示

cv::computeCorrespondEpilines

Stereo Calibration

上面已经说了很多的理论知识了所以我们现在就开始calibration吧！

• Stereo calibration是在空间上面计算两个相机的位置。相反，后面要说的rectification才是来保证两张图片行是共线的
• Stereo calibration主要依靠的是找两个相机之间的T和R矩阵，这两个都可以用cv::stereoCalibrate()来计算
  • 和单目相机的calibration有些相似，但是单目的相机要寻找一系列相机和chessboard之间的R和T
  • 双目的calibration在寻找唯一一个能让左右相机匹配上的R和T
• 可以得到三个等式求解
• 因为图片的noise或者rounding error，每组得到的结果可能会有轻微的不同，最后会取中位数
• calibration会把右边的相机放在和左边的相机相同的plane上面，这样这两个相机得到的图片就是parallel的，但是这时候还不是row-aligned的！！！
• 可以直接通过用这一个函数计算相机的intrinsic，extrinsic和Stereo的参数，不用先进行calibration

Stereo Rectification

• 如果两个图片aligned了，那么根据上面计算出来的disparity就可以很轻易的得到depth map了。但是在实际中只有相机没有这么容易做到
• 目标：我们需要reproject两个image plane，让他们在完全相同的plane里面，可以得到完美的aligned
• 我们希望在rectification之后图片的row aliged，这样stereo correspondence（在两个图片里找相同的点）就会变得更可信而且容易计算
  • 在另一张照片里只找match一个点的row
  • 这样的结果会有无限个待选
  • 我们再人为的加上限制
• 结果会有八个term，四个给左边的相机，四个给右边的相机（两种计算这些参数的算法）
  • 每个相机都会有distCoffs和旋转矩阵R，修正和未修正的相机矩阵（4个）
  • 用上面这些东西，得到map来确定原图要怎么修改cv::initUndistortRectifyMap()

Hartley’s algorithm + Bouguet’s algorithm（p730）

Rectification map

Stereo Correspondence

• 在两个图片里面match三维的点，只能在两张图片交叠的地方找到
• 两种不同的算法
  • block matching：快，效率高，基于“sum of absolute difference” (SAD）
    • 只会找到高度符合的点（highly textured）-> 户外
  • semi-global block matching (SGBM) ：精确度更高
    • matching is done at subpixel level using the Birchfield-Tomasi metric
    • enforce a global smoothness constraint on the computed depth information that it approximates by considering many one-dimensional smoothness constraints through the region of interest

Block matching

三个步骤

• prefiltering，normal图片的亮度，增强纹理
• 用SAD的窗口，搜索水平的epipolar line
  • 在rectificatin之后，每行都是一个epipolar line，所以左边的图片肯定在右边的同一行里面有一个对应的部分
  • disparity会在一定的pixel范围里进行搜索，不同范围里的disparity代表的是不同的depth。但是超过了最大值的话就找不到depth了 -> Each disparity limit defines a plane at a fixed depth from the cameras
• Postfiltering，减少比较差的结果

Semi-global block matching

code example （p752）

Structure from Motion

• 从移动中得到构造信息。但是在静止的情况下，一个相机移动得到的信息和两个相机得到的信息没有本质的区别
• 但是如果特别大的时候，就需要通过计算frame之间的关系得到最后的结果（SLAM？）
• 在附录

FitLine（直线拟合）

• 在三维的分析之中比较常用，所以在这里介绍