994 腐烂的橘子

2020.3.4
链接

在给定的网格中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。
每分钟，任何与腐烂的橘子（在 4 个正方向上）相邻的新鲜橘子都会腐烂。

返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 - 1。

基本思路

刚开始看到这道题感觉像是DP，因为要求的是最短时间，乍一看感觉是找一天最快的路径。但是仔细看了一下发现因为每次传播的时候，都同时向四个方向传播，每个的传播时间也相同，所以不存在最优路径的问题。这么想来的话应该是用BFS
基本流程如下：
- 在所有橘子腐烂之前，把上波新被传染的橘子放进Queue
- 遍历Queue里面的橘子，向这个橘子周围一周传染，判断是否有格子，传染结束之后从Queue里面移除
- 如果所有没有新的橘子可被感染，那么循环结束
实现中的判断如下：
- 首先遍历所有格子，得到有多少橘子和有多少腐烂的橘子。如果腐烂的橘子总数 == 橘子数，则说明所有的都被感染。反之，循环结束的时候如果没有都被感染，返回 - 1
- 判断跳出循环条件：没有新的橘子被感染，设定一个counter计算被新感染的橘子数，如果等于0则说明结束了
注意点
- 如果想从queue里面移除元素，可以用pop。如果用remove的话，需要在for的时候复制一个新的queue，否则报错

基本代码



def orangesRotting(self, grid: List[List[int]]) -> int:
    if not grid:
        return -1

    m, n = len(grid), len(grid[0])
    rotten = []
    org_num = 0  # 总数
    counter = 0  # 坏了的数量
    timer = 0

    # 第一次遍历找到坏了的
    for i in range(m):
        for j in range(n):
            if grid[i][j] == 2:
                rotten.append((i, j))
                org_num += 1
                counter += 1
            elif grid[i][j] == 1:
                org_num += 1
    # 开始扩散
    while rotten:
        # print(rotten)
        this_counter = 0
        for r in rotten[:]:
            candidate = [(r[0] - 1, r[1]), (r[0] + 1, r[1]),
                         (r[0], r[1] - 1), (r[0], r[1] + 1)]
            for a in candidate[:]:
                if a[0] < 0 or a[0] >= m:
                    candidate.remove(a)
                elif a[1] < 0 or a[1] >= n:
                    candidate.remove(a)
            for a in candidate:
                if grid[a[0]][a[1]] == 1:
                    grid[a[0]][a[1]] = 2
                    rotten.append((a[0], a[1]))
                    counter += 1
                    this_counter += 1
            rotten.remove(r)
        if this_counter > 0:
            timer += 1
        # print(rotten,timer)
    if counter == org_num:
        return timer
    else:
        return -1

希望改进的地方

remove的用法感觉有点丑陋，counter的用法也有点丑陋
- 可以不用while里面的那个counter，直接用queue是否为空来判断
- 使用pop -> 但是这个不是一个一个判断而是每次会有好几个腐烂的橘子，所以pop不太好用
判断在不在格子里感觉也有点丑陋，能不能在这个格子周围加一圈？
- 设定一个四个元素的list来表示这个格子的四周
最后的判断方法也优点丑陋
- 其实可以直接判断最后的结果里面有没有1，但是这样的话需要增加一次对整个矩阵的循环。但用个数判断也无可厚非



def orangesRotting(self, grid: List[List[int]]) -> int:
    if not grid:
        return -1

    m, n = len(grid), len(grid[0])
    rotten = []
    org_num = 0  # 总数
    counter = 0  # 坏了的数量
    timer = 0

    D = [[1, 0], [-1, 0], [0, 1], [0, -1]]  # 找到周围的点

    # 第一次遍历找到坏了的
    for i in range(m):
        for j in range(n):
            if grid[i][j] == 2:
                rotten.append((i, j))
                org_num += 1
                counter += 1
            elif grid[i][j] == 1:
                org_num += 1
    # 开始扩散
    while rotten:
        this_counter = 0
        for r in rotten[:]:
            i, j = r[0], r[1]
            for d in D:
                mat_i, mat_j = i + d[0], j + d[1]
                if 0 <= mat_i < m and 0 <= mat_j < n and grid[mat_i][mat_j] == 1:
                    grid[mat_i][mat_j] = 2
                    rotten.append((mat_i, mat_j))
                    counter += 1
                    this_counter += 1
            rotten.remove(r)
        if this_counter > 0:
            timer += 1
    if counter == org_num:
        return timer
    else:
        return -1

1103 分糖果2

2020.03.05
链接

排排坐，分糖果。

我们买了一些糖果 candies，打算把它们分给排好队的 n = num_people 个小朋友。

给第一个小朋友 1 颗糖果，第二个小朋友 2 颗，依此类推，直到给最后一个小朋友 n 颗糖果。

然后，我们再回到队伍的起点，给第一个小朋友 n + 1 颗糖果，第二个小朋友 n + 2 颗，依此类推，直到给最后一个小朋友 2 * n 颗糖果。

重复上述过程（每次都比上一次多给出一颗糖果，当到达队伍终点后再次从队伍起点开始），直到我们分完所有的糖果。注意，就算我们手中的剩下糖果数不够（不比前一次发出的糖果多），这些糖果也会全部发给当前的小朋友。

返回一个长度为 num_people、元素之和为 candies 的数组，以表示糖果的最终分发情况（即 ans[i] 表示第 i 个小朋友分到的糖果数）。

基本思路：遍历

while candies大于0就一直分
对每个小孩，每次需要的糖果量是轮数 * n + 小孩的位置
- 如果够，分给小孩，继续给下一个
- 如果不够，全都给小孩，然后break



class Solution:
    def distributeCandies(self, candies: int, num_people: int) -> List[int]:
        ans = [0 for i in range(num_people)]
        counter = 0
        while candies > 0:
            for i in range(1, num_people + 1):
                candy_need = counter * num_people + i
                if candy_need >= candies:
                    ans[i - 1] += candies
                    candies = 0
                    break
                elif candy_need < candies:
                    ans[i - 1] += candy_need
                    candies -= candy_need
            counter += 1
        return ans

面试题57-2 和为s的正整数序列

2020.03.06
链接

输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。
序列内的数字由小到大排列，不同序列按照首个数字从小到大排列。

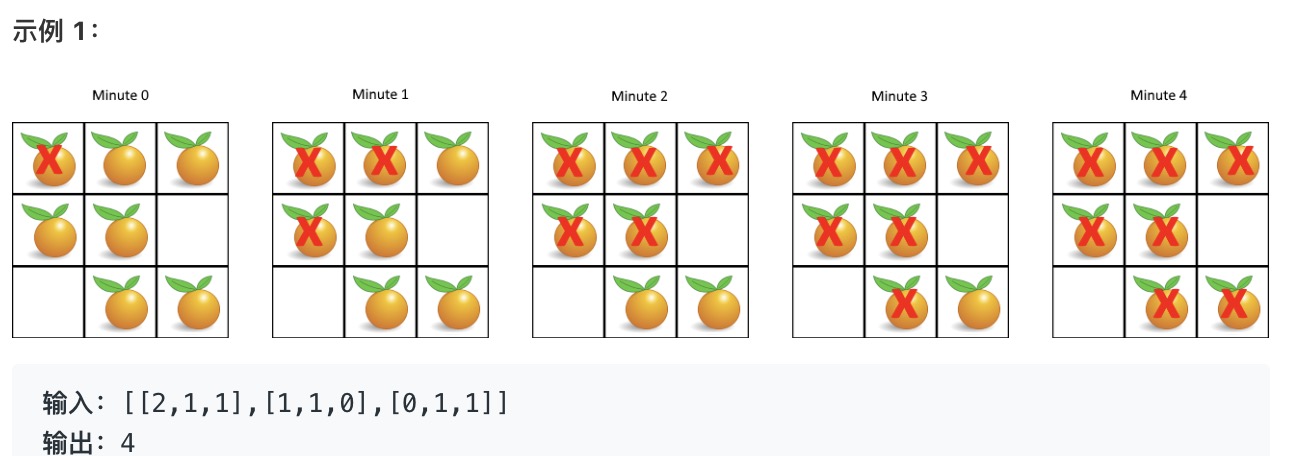
示例 1：

输入：target = 9
输出：[[2,3,4],[4,5]]

自己的思路：数学解法

从结果上来看，其实就是给等差数列求和，（首项+末项）* 项数 / 2
那么首先从2开始到target遍历项数
- 从数学的角度来说这个应该可以进一步缩减数量，但是为了简单我就直接遍历到target了
- 注意这里不是从1开始，如果从1开始的话，单个的数字也会被算进去。但是题目要求的是两个及以上的数字
如果可以整除，那么整除的结果应该是 2 首项 + 项数 - 1*。因为是连续数字
这样的话，如果里面可以给首项取整，且首项需要大于0，就能得到相对应的值了。这里我最开始写错了，首项是不需要遍历的
注意我这里的项数从2开始遍历的，所以得到的结果顺序和需要的顺序是反着的，可以从target开始遍历。

def findContinuousSequence(self, target: int) -> List[List[int]]:
        result = []
        for num_item in range(target,1,-1):
            if target*2%num_item == 0:
                new_target = int(target*2 / num_item)
                first = new_target + 1 - num_item
                if first > 0 and first%2 == 0:
                    first = int(first/2)
                    result.append([first+i for i in range(num_item)])
        return result

另一种思路：滑动窗口

滑动窗口可以来解决字符串或者数组的元素问题，他可以把循环的嵌套的时间复杂度降到单次循环。其实也可以理解成两个pointer的方法。两个pointer只能往右边移动，这样一次遍历就可以访问所有结果

窗口有几种可能：

如果现在的值比target小，右pointer向右移动
如果现在的值比target大，左pointer向右移动（减小和）

如果相等，记录这个值，左pointer向右移动

def findContinuousSequence(self, target: int) -> List[List[int]]:
        result = []
        i,j = 1,1
        while i < target:
            temp = (i+j)*(j-i+1)/2
            if temp < target:
                j += 1
            elif temp > target:
                i += 1
            elif temp == target:
                result.append([a for a in range(i,j+1)])
                i += 1
        return result

因为这里只考虑自然数，不用考虑角标，所以i和j从1开始比从0开始更方便

延伸阅读，面试题57

输入一个递增排序的数组和一个数字s，在数组中查找两个数，使得它们的和正好是s。如果有多对数字的和等于s，则输出任意一对即可。
链接

之前做滑动块那个做傻了，这个一次还没做出来。
基本思路1是暴力遍历，基本思路2是双指针。但是注意的是双指针需要找到这个题里面需要的规律。比如这个的里面双指针就是一前一后两个指针，不能一起在前面
- 如果相等，输出
- 如果大于，j向左移动一位
- 如果小于，i向右移动一位

def twoSum(self, nums: List[int], target: int) -> List[int]:
        i,j = 0,len(nums) - 1
        while i < j:
            if nums[i] + nums[j] == target:
                return [nums[i],nums[j]]
            elif nums[i] + nums[j] > target:
                j -= 1
            elif nums[i] + nums[j] < target:
                i += 1
        return []

面试题59-2 实现队列的最大值

2020.03.07
链接

请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数max_value、push_back 和 pop_front 的时间复杂度都是O(1)。

若队列为空，pop_front 和 max_value 需要返回 -1

示例 1：

输入:
[“MaxQueue”,”push_back”,”push_back”,”max_value”,”pop_front”,”max_value”]
[[],[1],[2],[],[],[]]
输出: [null,null,null,2,1,2]

分析

如果本身来说实现起来非常简单。push和pop的复杂度都可以做到O(1)，但是遍历寻找最大值的复杂度是O(n)
降低复杂度一共就那么几个思路：第一个是用一个变量来记录最大值，但是这样的话当前最大值如果被pop出去了之后，就无法确定最大值了。第二个就是用空间换时间，使用了一个deque来实现最大值的记录（自己并没有想出来）

此题思路

这道题和上面的stack的区别在于queue需要从前面pop出来，所以如果push 2，1。pop 2的时候，按上面一道题的方法辅助数组里面就没有东西了
所以这道题的辅助数组构建应该是从前到后依次减小
- 如果新push的数字大于辅助数组的最后，则把辅助数组最后一直删除，直到可以放下新的数字。比如 2，1，1，1，3的时候，辅助数组在放3之前是2，1，1，1。但是很明显可以发现，当popleft的时候，如果新的数组里有了3，则之前的2111对最大值就没有了影响。
- 在pop的时候，如果pop的数字和辅助数组的最左边相同，则辅助数组一起popleft
注意，pop(i)的复杂度是O(n)，包括pop(0)，所以用的时候最好还是建立一个deque然后用popleft的功能

from collections import deque
class MaxQueue:

    def __init__(self):
        self.queue = deque()
        self.assist_queue = deque()


    def max_value(self) -> int:
        if not self.queue:
            return -1
        return self.assist_queue[0]
        


    def push_back(self, value: int) -> None:
        self.queue.append(value)
        while self.assist_queue and value > self.assist_queue[-1]:
            self.assist_queue.pop()
        self.assist_queue.append(value)



    def pop_front(self) -> int:
        if not self.queue:
            return -1
        temp =  self.queue.popleft()
        if temp == self.assist_queue[0]:
            self.assist_queue.popleft()
        return temp

322 零钱兑换

链接

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

思路分析

很标准的动态规划题，直接暴力解法的话肯定会爆炸。动态规划由上至下或者由下而上都可以实现
这里的时间复杂度应该是 amout * coins，数字的总数乘以不同的额度数。另一个需要考虑到的点是因为不一定有1块的额度，所以可能拼不出来需要的数据
边缘情况：额度为0，coins为空

自下而上的思路代码

这里踩到了坑主要是我把无法组成数字的位置设定为None，但是组成的硬币枚数为0的时候也表示否，所以not None和not 0都会被判断为true

建立一个大小为amout的数组，每个位置上记录可以组成这个数字的最小枚数。对一个新的数字来说，遍历所有coin的面值，得到一个最小的面值。如果所有的面值都没法得到，则这个数字也没法得到

def coinChange(self, coins: List[int], amount: int) -> int:
        # 边缘情况：没有coins，不行。没有amount，返回0
        if not coins: return -1
        result = [None for i in range(amount+1)]
        result[0] = 0
        for i in range(1,amount+1):
            min_coin = float("inf")
            for c in coins:
                if (i - c >= 0) and (result[i-c] is not None): 
                    min_coin = min(min_coin,result[i-c]+1)
            if min_coin == float("inf"):
                result[i] = None
            else:
                result[i] = min_coin
        if result[amount] is not None: return result[amount]
        else: return -1

在上面代码的基础上，可以直接把inf和None认为成一种情况，这样代码可以进一步简化

不用判断result[i-c]是不是None了，因为如果是None，这个值等于inf，那么放在min里面比较的时候也会直接比较出来。

最后返回结果的时候也可以判断是不是inf，是inf就是不行。注意这里要用等于来判断

def coinChange(self, coins: List[int], amount: int) -> int:
        # 边缘情况：没有coins，不行。没有amount，返回0
        if not coins: return -1
        result = [float("inf") for i in range(amount+1)]
        result[0] = 0
        for i in range(1,amount+1):
            for c in coins:
                if (i - c >= 0): 
                    result[i] = min(result[i],result[i-c]+1)
        if result[amount] != float("inf"): return result[amount]
        else: return -1

自上而下的算法

参考了评论区的算法，主要是return写在一行python比较占便宜

使用 functools 模块的 lur_cache 装饰器，可以缓存最多 maxsize 个此函数的调用结果，从而提高程序执行的效率，特别适合于耗时的函数，不使用的时候会超时（None为没有限制）

def coinChange(self, coins: List[int], amount: int) -> int:
        import functools
        @functools.lru_cache(None)
        def recursion(n):
            if n == 0:
                return 0
            return min(recursion(n-c) if n - c >= 0 else float("inf") for c in coins)+ 1
        if not coins: return -1
        result = recursion(amount)
        return result if result != float("inf") else -1

121 买卖股票的最佳时机 2020.03.09

链接

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

基本思路

只能买卖一次，所以其实求的就是这个数组里面后面的数字和前面的数字的最大的差值
第一思路，建造一个大小为n天的数组，每个位置上面记录这一天之前的最小的数字。然后用这天的数字减去最小的数字，就是这天的差值，然后在所有差值里面找最大的
进一步简化：因为之前的最小值只会随着时间而减小，而利润的最大值只会随着时间而增大，所以并不需要数组来记录这个结果，可以直接用两个变量来记录结果

def maxProfit(self, prices: List[int]) -> int:
    if not prices: return 0
    MAXProfit = 0 #记录最大利润
    minPrice = prices[0] #记录最小值
    for i in range(1,len(prices)): #从第二天开始，因为不能当天买卖
        MAXProfit = max(MAXProfit, prices[i]-minPrice)
        minPrice = min(minPrice,prices[i]) #这天价格*之前*的最小值
    return MAXProfit

543 二叉树直径 2020.03.10

链接
给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过根结点。

整体思路

在我最开始思考这道题的时候，我想的是求出两个子树的深度就可以了。但是实际上我理解错了，这个树不一定是完全二叉树。在不是完全二叉树的情况下，可能会有的点为Null，然后这个树不进行下去，所以需要找到就是最深的一条路先，即取max
关于点和路径
- 在这道题的计算中，要清楚是计算点还是计算线
- 每次计算路径的时候，线是比点少1的
- 每次计算深度的时候，需要计算的是两个子树的点树，在加上Root的一个点，即L+R+1，最后求出来的树的最长路径应该是d-1（点树-1）
边缘情况：当树为空的时候，路径长度为0
深度计算：
- def一个新的函数来计算这个root下面的深度
- 边缘条件：root为空的时候，长度返回0
- recursive左右的子树，得到最长的深度
路径计算：
- 因为不一定每次的最深子树得到的都是最长的路径，所以定义了一个全局变量来记录路径
- path = max(path,R+L+1)，如果现在这个点得到的最大路径大于以前的路径，则更新最大路径

代码实现

def diameterOfBinaryTree(self, root: TreeNode) -> int:
    self.d = 1
    if not root: return 0
    # return self.calcultateDepth(root.left) + self.calcultateDepth(root.right)
    self.calcultateDepth(root)
    return self.d - 1

import functools
@functools.lru_cache(None)
def calcultateDepth(self,root):
    if not root:
        return 0
    L = self.calcultateDepth(root.left)
    R = self.calcultateDepth(root.right)
    self.d = max(L+R+1,self.d)
    return max(L,R)+1

1013 数组分为和相等的三部分 2020.03.11

链接
给你一个整数数组 A，只有可以将其划分为三个和相等的非空部分时才返回 true，否则返回 false。

形式上，如果可以找出索引 i+1 < j 且满足 (A[0] + A[1] + … + A[i] == A[i+1] + A[i+2] + … + A[j-1] == A[j] + A[j-1] + … + A[A.length - 1]) 就可以将数组三等分。

整体思路

首先，需要注意审题。需要分成三个和相等的序列，且每个部分是连续的。那么每个部分的和都应该是这个数组的和的三分之一
从最初开始遍历数组，如果前i个数字的和是这个三分之一，则继续计算第二部分。如果第二部分也是，那么这个数组符合要求
- 注意这里第三部分不用再求了。因为已经求出来的target就是这个数组的平均值，如果第一第二部分都符合平均值，那么第三部分则不用再求了
注意代码简洁

代码实现

下面的代码写了两种方法，思路是一样的，但是comment了的那种看起来更简洁一点

def canThreePartsEqualSum(self, A: List[int]) -> bool:
    if not A or len(A) < 3: return False
    s = sum(A)
    if s % 3 != 0: return False
    target = s//3
    # i,n,cur = 0,len(A),0
    # while i < n:
    #     cur += A[i]
    #     if cur == target:
    #         break
    #     i += 1
    # if cur != target:
    #     return False
    # j = i+1
    # while j < n-1:
    #     cur += A[j]
    #     if cur == 2*target:
    #         return True
    #     j+=1
    # return False

        
    target_1 = target_2 = target
    i,j = None, None
    for a in range(len(A)):
        target_1 -= A[a]
        if target_1 == 0:
            i = a
            break
    if i == 0 or i:
        for a in range(i+1,len(A)):
            target_2 -= A[a]
            if target_2 == 0:
                j = a
                break
    if j and j<len(A)-1:
        return True 
    return False

字符串的最大公因子 2020.03.12

链接

对于字符串 S 和 T，只有在 S = T + … + T（T 与自身连接 1 次或多次）时，我们才认定 “T 能除尽 S”。

返回最长字符串 X，要求满足 X 能除尽 str1 且 X 能除尽 str2。

示例 1：

输入：str1 = “ABCABC”, str2 = “ABC”
输出：”ABC”

基本思路

这里需要注意，题的名字里就呆着gcd，所以求得时候也和gcd非常相似。这里需要复习一下辗转相除法求gcd。有ab两个数字，每次新输入的数字是b和a%b，如果a%b==0的时候，现在的b就是最大公因数
注意，两个str都是重复的，所以每个str都应该是被gcd填满的
先求gcd的长度，这个长度的求法就是用辗转相除两个str的长度len
其次验证结果是不是：
- 如果结果符合，对任意str来说，前len个位就应该是需要求的结果
- 如果结果符合，那么这个结果*（str总长度//gcd）长度应该就和以前的字符串相同

思路拓展

如果 str1 和 str2 拼接后等于 str2和 str1 拼接起来的字符串（注意拼接顺序不同），那么一定存在符合条件的字符串 X。
- 所以可以先判断有没有gcd
- 如果有的话，对两个str的长度求gcd，前这个位数就是结果

class Solution:
    def gcdOfStrings(self, str1: str, str2: str) -> str:
        m,n = len(str1),len(str2)
        length_result = self.gcd(m,n)
        result = str1[:length_result]
        if result * (m//length_result) == str1 and result * (n//length_result) == str2:
            return result
        return ""
    
    def gcd(self,a,b):
        if b == 0:
            return a
        return self.gcd(b,a%b)

169 多元数组 2020.03.13

链接

给定一个大小为 n 的数组，找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

思路1（没有写代码）

排序，看中间这个是不是。
因为这道题已经确定了数组里面肯定有这个结果，在极端情况下，多数元素也应该出现在中间这位上面。所以可以直接排序

思路2 hash

如果仅仅使用遍历来求解，那么需要的时间复杂度是n2。但是可以直接用dict来一次遍历计数成功

注意求dict里面value最大时候key的值的写法，活用lambda

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        result = {}
        for n in nums:
            if n not in result:
                result[n] = 1
            else:
                result[n] += 1
        # max(result,key = lambda x: x[1])
        return max(result,key = result.get)

扩充思路：Boyer-Moore投票算法

时间复杂度n，遍历一次。空间复杂度1，不需要额外的空间。
维护一个变量candidate和一个投票值vote
遍历一次数组
- 当vote等于0的时候，把当前数字赋给candidate
- 判断如下条件：
  - 如果当前值等于candidate，那么vote+1
  - 如果当前值不等于candidate，那么vote-1
遍历之后剩下的candidate就是要求的值
可以认为最后的结果的值投票的时候都投正的，非结果的值投票的时候都投反的。因为结果本身是大于一半的数字，所以留下的永远都是要求的结果。

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        candidate = nums[0]
        vote = 0
        for n in nums:
            if vote == 0:
                candidate = n
            if candidate == n:
                vote += 1
            else:
                vote -= 1
        return candidate

300 最长上升子序列 2020.03.14

链接

给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例:

输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

思路1，DP

时间复杂度n2，需要进行两个嵌套的遍历
最长上升子序列的定义：子序列不一定是连续的，所以不能直接用一个变量记录最长的长度
创建一个辅助数组，大小和nums相同，记录的是：以这一位结尾的时候，这个数组的LIS的最长长度。

状态转换公式

当以i位结束时，对比这一位和前面的i位的大小，如果这位比前面i位里面的j大，那么说明这位可以加到新的LIS里面去，这位截止的长度是max(length[i],length[j]+1)

如果遍历了所有他前面的位数，都没有比他小的，那么这一位只能作为一个新的LIS的起点，长度为1。由此思考辅助数组的所有位可以直接初始化为1

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums: return 0
        n = len(nums)
        maxLength = [1 for i in range(n)]   #记录以这位结尾的时候可以拥有的最大长度
        for i in range(1,n):
            for j in range(0,i):
                if nums[i] > nums[j]:
                    maxLength[i] = max(maxLength[i],maxLength[j]+1)
        return max(maxLength)

思路2：贪心+二分查找

对于给定的字符串，还可以进行进一步的优化。考虑到贪心的策略，每次加到LIS里面的最后一个数字都要尽可能的小，这样增长的速度才可以尽可能的小
创建一个辅助数组d[i]，来记录在长度为i的时候，LIS最后一位可以保持的最小值，用len记录这个上升数组的长度
在这里需要注意的是，d[i]是对i单调递增的（可证）
遍历整个数组，更新d和len的值。如果现在的nums[i] > d[len]，那么len++。否则在1到len里面寻找满足d[k-1]< nums[i] < d[k]的下标k，并且更新d[k] = nums[i].
根据数组单调性，可以二分查找寻找下标，复杂度为logn

进一步解析

实际上，数组d记录的就是长度为len的时候，这个时候LIS最小的尾部元素。
- 在最初的时候，d的内容就只有nums里面的第一位
- 遍历所有数组，当当前数字比d的最后一位还大的时候，直接夹加在d的最后
- 当这个数字比最后一位小的时候，采用二分查找，找到一个可以塞进这个数字的地方，替换之前的数字。也就是说：在长度不变的情况下，把之前的比较大的尾部元素的值采用二分查找刷新成了更新的尾部元素的值

最后返回的值就是LIS的最大值：

即：新数比前面都大的时候，长度加一
新数小于前面的任意长度的时候，替换前面的长度。

可以直接跟尾部数字比，是因为d这个数组单调递增的特性


class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums: return 0
        n = len(nums)
        d = [nums[0]]
        for i in range(1,n):
            if nums[i] > d[-1]:
                d.append(nums[i])
            else:
                l,r = 0,len(d) - 1
                loc = r 
                while l <= r:
                    mid = (r+l)//2
                    if d[mid] >= nums[i]:
                        loc = mid
                        r = mid-1
                    else:
                        l = mid+1
                d[loc] = nums[i]
        return len(d)

409 最长回文串

给定一个包含大写字母和小写字母的字符串，找到通过这些字母构造成的最长的回文串。

在构造过程中，请注意区分大小写。比如 “Aa” 不能当做一个回文字符串。

注意:
假设字符串的长度不会超过 1010。

思路：

注意这这道题是在s里面自由组合
回文的定义是正着读和反着读都一样的文字，所以根据定义可以发现，回文里面有两种情况：
- 所有数字出现的次数都是偶数次
- 只有一个数字出现的是奇数次，剩下的都是偶数次
遍历所有的字母，统计每个字母出现的次数。可以用collections.Counter来实现
对于每个字字母来说，增加的长度是这个字母出现的次数v，的v//2 * 2。即如果是偶数个的话就都加进去，如果是奇数个的话就加偶数个
当整体长度为偶数，且新的字母为奇数的时候，可以再加上一位。但是注意这个只加一次，加了之后整体的长度就是奇数位了

class Solution:
    def longestPalindrome(self, s: str) -> int:
        res = 0
        counter = collections.Counter(s)
        for v in counter.values():
            res += v // 2 * 2
            if res % 2 == 0 and v % 2 == 1:
                res += 1
        return res

leetcode每日一题挑战

994 腐烂的橘子

基本思路

基本代码

希望改进的地方

1103 分糖果2

基本思路：遍历

面试题57-2 和为s的正整数序列

自己的思路：数学解法

另一种思路：滑动窗口

延伸阅读，面试题57

面试题59-2 实现队列的最大值

分析

相关参考

此题思路

322 零钱兑换

思路分析

自下而上的思路代码

自上而下的算法

121 买卖股票的最佳时机 2020.03.09

基本思路

543 二叉树直径 2020.03.10

整体思路

代码实现

1013 数组分为和相等的三部分 2020.03.11

整体思路

代码实现

字符串的最大公因子 2020.03.12

基本思路

思路拓展

169 多元数组 2020.03.13

思路1（没有写代码）

思路2 hash

扩充思路：Boyer-Moore投票算法

300 最长上升子序列 2020.03.14

思路1，DP

思路2：贪心+二分查找

进一步解析

409 最长回文串

思路：